5 Essential Tips for Mastering Exponents in Math

Understanding and mastering exponents can significantly enhance your mathematical abilities, opening up a world of possibilities in algebra, calculus, calculus, physics, and even computer science. Exponents, or powers, allow you to express numbers in a compact and elegant form, which can be particularly useful when dealing with extremely large or small numbers. Here are five essential tips to help you become proficient in working with exponents:
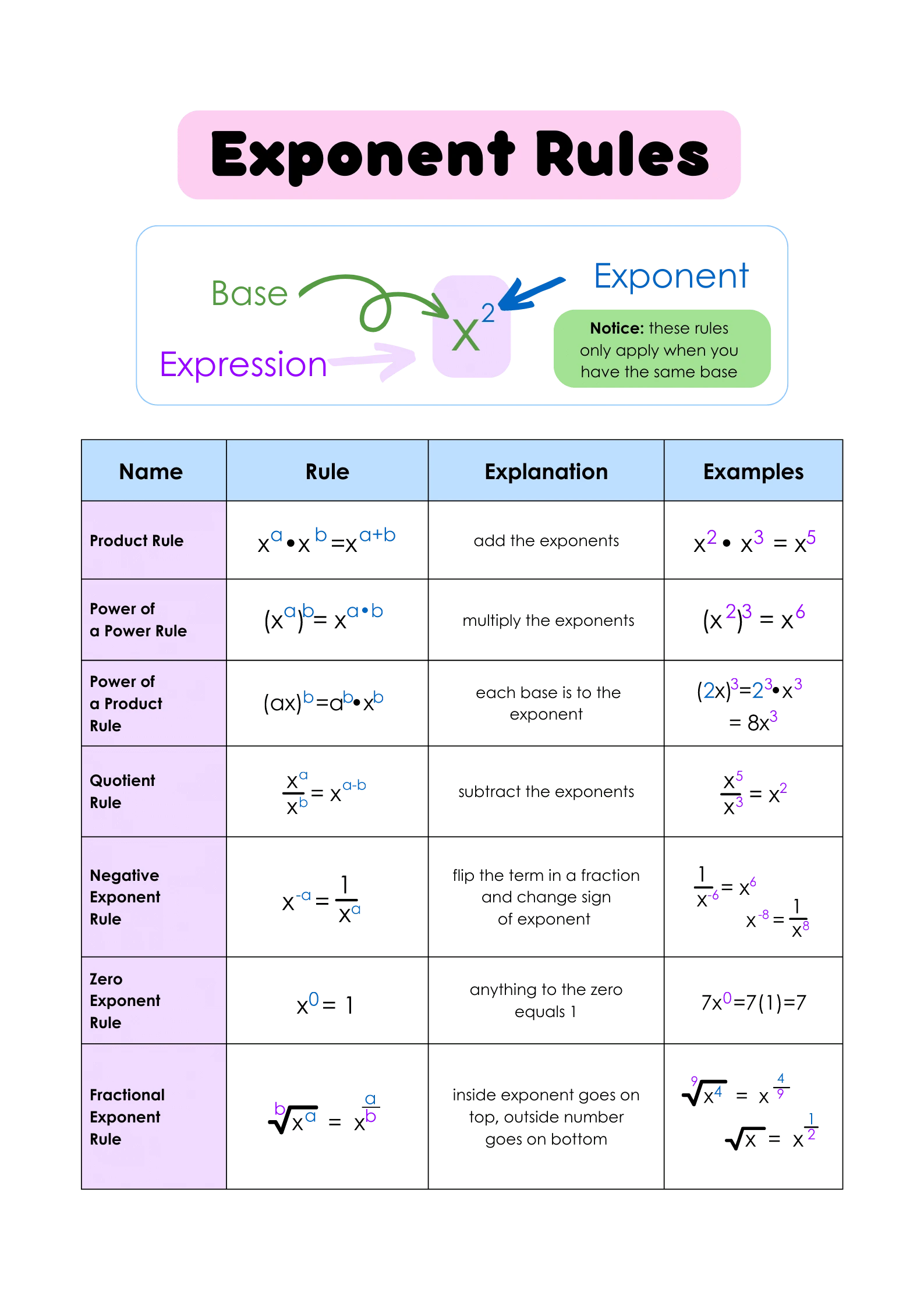
1. Understand the Basics

Before diving into complex exponent operations, make sure you have a solid grasp of the fundamental concepts:
- What is an exponent? An exponent represents how many times you multiply a number by itself. For example, in 3^4, 3 is the base, and 4 is the exponent.
- Negative Exponents: a^{-n} = \frac{1}{a^n}. A negative exponent means the reciprocal of the base raised to the positive exponent.
- Zero Exponent: Any non-zero number raised to the power of zero is 1 (i.e., a^0 = 1, where a \neq 0).
Visual Aid:


Memorize these properties:
- Product of Powers: (a^m)(a^n) = a^{m+n}
- Quotient of Powers: \frac{a^m}{a^n} = a^{m-n} (where a \neq 0)
- Power to a Power: (a^m)^n = a^{mn}
🚀 Note: Understanding these basic rules is crucial as they form the foundation for solving more complex exponential problems.
2. Master Exponential Operations

Once you understand the basics, practice with exponential operations:
- Addition and Subtraction: When adding or subtracting powers, you can only do so if the exponents are the same. For example, 3^2 + 3^2 = 2 \times 3^2 = 18.
- Multiplication and Division: Use the rules mentioned above to multiply or divide exponents. E.g., (x^3)(x^2) = x^{5} or \frac{x^5}{x^2} = x^{3}
- Exponentiation: Raising an exponential expression to another power requires multiplying the exponents. For example, (2^3)^2 = 2^{3 \times 2} = 2^6.
Table of Exponential Operations:
| Operation | Example | Result |
|---|---|---|
| Addition | 3^2 + 3^2 | 18 |
| Multiplication | (x^3)(x^2) | x^5 |
| Division | \frac{x^5}{x^2} | x^3 |
| Exponentiation | (2^3)^2 | 2^6 |

3. Simplify Exponential Expressions

Simplifying exponential expressions can make calculations easier:
- Combine Like Terms: When dealing with variables and exponents, combine terms with the same base. E.g., 3x^2 + 2x^2 = 5x^2.
- Use Properties: Apply the properties of exponents to simplify expressions. For example, \frac{27^3}{9} = \frac{(3^3)^3}{3^2} = 3^{9 - 2} = 3^7.
Examples of Simplification:

- 125^{1/3} = 5
- \sqrt[3]{8x^3} = 2x
4. Work with Fractional and Negative Exponents

Understanding fractional and negative exponents is vital for handling complex mathematical expressions:
- Fractional Exponents: a^{m/n} = \sqrt[n]{a^m} (n-th root of a^m). Example: 27^{1/3} = \sqrt[3]{27} = 3.
- Negative Exponents: As mentioned before, a^{-n} = \frac{1}{a^n}. This can be used to simplify expressions like \frac{1}{5^{-2}} = 5^2 = 25.
Examples:

- 16^{3/4} = \sqrt[4]{16^3} = \sqrt[4]{4096} = 8
- 2^{-3} = \frac{1}{2^3} = \frac{1}{8}
5. Utilize Exponents in Real-World Applications

Exponents are not just theoretical; they have practical applications in science and technology:
- Scientific Notation: Used to express very large or very small numbers. For instance, the speed of light is approximately 2.998 \times 10^8 meters per second.
- Growth and Decay: Exponents model growth (like compound interest) or decay (like radioactive half-life).
- Computer Science: Binary arithmetic uses exponents to denote the place values in binary.
📝 Note: Practicing real-world problems will reinforce your understanding and help you apply exponents in practical scenarios.
Summary:

Mastering exponents involves a deep understanding of basic rules, practicing exponential operations, simplifying expressions, dealing with fractional and negative exponents, and applying these concepts in real-life situations. This holistic approach ensures that your skills are not only academic but also practically useful.
What is the difference between a coefficient and an exponent?

+
A coefficient multiplies the variable, while an exponent raises the variable to a power. For example, in the term (2x^3), 2 is the coefficient, and 3 is the exponent.
Can exponents be fractions or decimals?

+
Yes, exponents can be fractions or decimals. A fractional exponent like (a^{m/n}) means the nth root of (a^m), while a decimal exponent can be interpreted similarly, though often approximated by a rational approximation.
How do you simplify an expression with both negative and positive exponents?

+
You first separate the negative and positive terms, converting negative exponents into positive by taking the reciprocal of the base. Then combine like terms where possible.
Why is zero exponent equal to one?

+
Any number (except zero) raised to the zero power is defined as one because any number divided by itself equals one, following the property (a^m/a^n = a^{m-n}) where if (n = m), (a^0 = 1).
What are the common mistakes when working with exponents?

+
Common mistakes include adding or subtracting exponents incorrectly, confusing exponents with coefficients, and forgetting the signs when dealing with negative exponents.



