5 Ways to Master Fractions with Math-aids Worksheets

Mastering fractions is a critical skill in mathematics, offering a foundation for understanding more complex concepts like algebra, decimals, and even calculus. Many students struggle with fractions due to their abstract nature, but fear not! With the right tools and practice, anyone can conquer this seemingly daunting subject. Today, we dive into five foolproof strategies to master fractions using Math-aids Worksheets.
1. Understanding the Basics
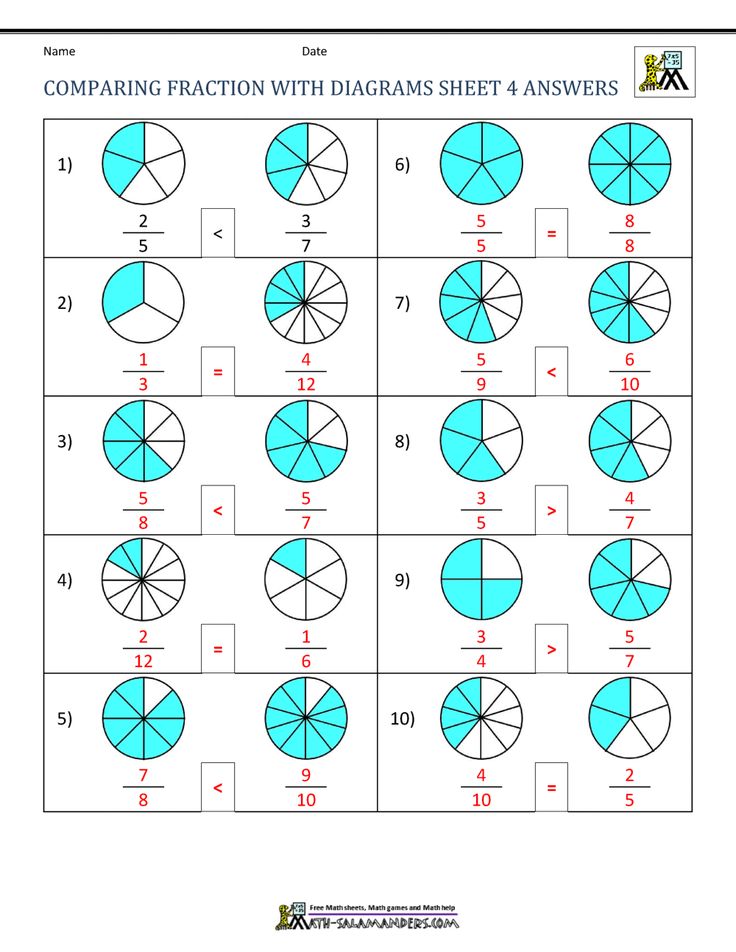
Before diving into complex fraction problems, it’s essential to grasp the basics. Math-aids Worksheets offers:
- Interactive definitions and visual explanations of what fractions are.
- Worksheets focused on identifying and naming fractions, helping learners to understand the numerator and denominator’s roles.
- Exercises for converting mixed numbers to improper fractions and vice versa.
By using these worksheets, students can become comfortable with the building blocks of fractions. For example, exercises might ask students to identify which part of a whole is represented by a fraction, helping to solidify their conceptual understanding.
2. Practicing Addition and Subtraction
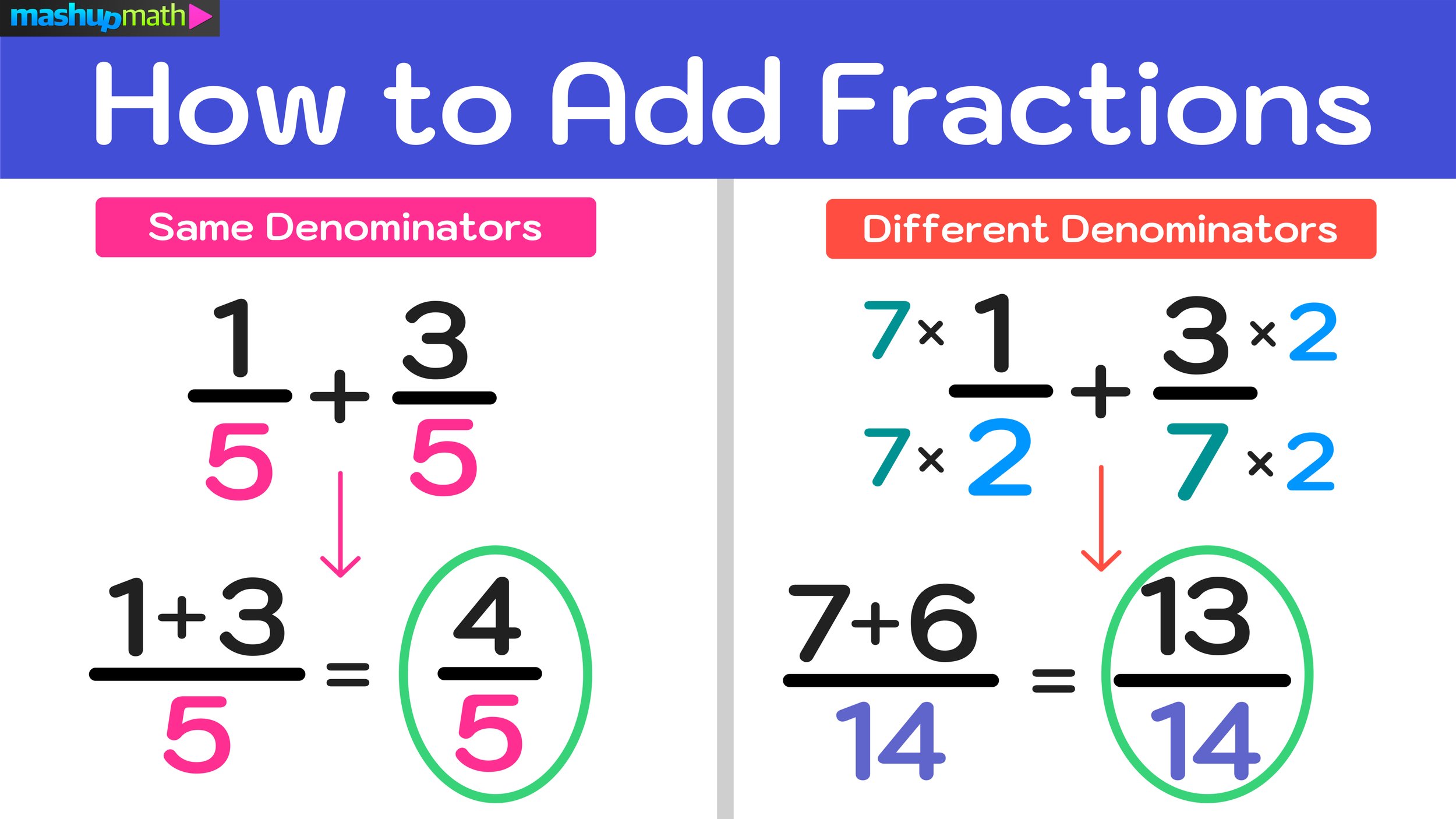
One of the earliest and most fundamental operations in fractions is addition and subtraction. Here’s how Math-aids Worksheets can help:
- Guided worksheets that start with like denominators, introducing the concept of adding and subtracting fractions easily.
- Progressive worksheets that introduce unlike denominators, teaching students to find common denominators, making these operations more accessible.
- Visual aids to show the equivalence of fractions, simplifying the process of finding common ground.
A typical exercise might involve adding fractions with like denominators such as ( \frac{1}{4} + \frac{1}{4} ) or moving on to unlike denominators like ( \frac{3}{5} + \frac{1}{3} ).
3. Multiplication and Division Mastery
Multiplying and dividing fractions can be challenging, but Math-aids Worksheets simplify this through:
- Worksheets that teach how to multiply fractions by fractions, whole numbers, and mixed numbers.
- Exercises for dividing fractions, including the ‘flip and multiply’ method, making division intuitive.
- Word problems that contextualize multiplication and division of fractions, showing real-life applications.
For instance, worksheets might include problems like ( \frac{2}{3} \times \frac{4}{5} ) or ( \frac{1}{2} \div \frac{2}{3} ), providing clear, step-by-step guidance through these operations.
4. Simplifying Fractions

Simplification is a skill that leads to cleaner, more manageable arithmetic. Here’s how to use Math-aids Worksheets for this:
- Exercises that introduce the Greatest Common Divisor (GCD) for simplifying fractions.
- Guided steps for students to simplify both proper and improper fractions.
- Challenges where students must simplify fractions before performing operations for streamlined calculation.
For example, a worksheet might include ( \frac{12}{18} ) and ask students to simplify it to ( \frac{2}{3} ).
🔔 Note: Remember, when simplifying fractions, the numerator and denominator are divided by the same number to maintain the fraction’s value.
5. Real-World Applications

Applying fractions to real-life situations can help students see their importance and relevance. Here’s how:
- Word problems involving cooking, finance, or DIY projects, making fractions relatable.
- Worksheets that blend fractions with units of measurement, like converting feet to inches or pounds to ounces.
- Games and puzzles that require fraction manipulation, enhancing problem-solving skills.
These worksheets might simulate scenarios like splitting a pizza among friends or adjusting a recipe for more servings, requiring the use of addition, subtraction, multiplication, and division of fractions in context.
In our journey to master fractions, Math-aids Worksheets have proven to be an invaluable resource. They provide not just practice but a structured approach to learning fractions. From understanding the basics to applying these concepts in real-world scenarios, these worksheets make learning fun, engaging, and effective. With persistent practice and the right tools, fractions become a tool rather than an obstacle, empowering students to solve problems, comprehend ratios, and prepare for higher mathematics confidently. Remember, the key to mastering fractions is practice, patience, and making connections between what you're learning and the world around you.
What are the basic types of fractions I should know?

+
There are several types of fractions to be familiar with: Proper fractions (where the numerator is less than the denominator), improper fractions (where the numerator is greater than or equal to the denominator), mixed numbers (which combine a whole number and a proper fraction), and equivalent fractions (fractions that represent the same value).
How can I convert a mixed number into an improper fraction?
+
Multiply the whole number by the denominator of the fraction part, add the numerator, and then place this over the original denominator. For example, for ( 2 \frac{3}{4} ), you’d multiply 2 by 4 (which gives you 8), add 3 (which gives you 11), then put 11 over 4, resulting in ( \frac{11}{4} ).
Why is it important to simplify fractions?

+
Simplifying fractions reduces the numbers to their smallest form, which makes further operations and comparisons easier and reduces the chance for errors in calculations. It also helps in understanding the concept of equivalent fractions.