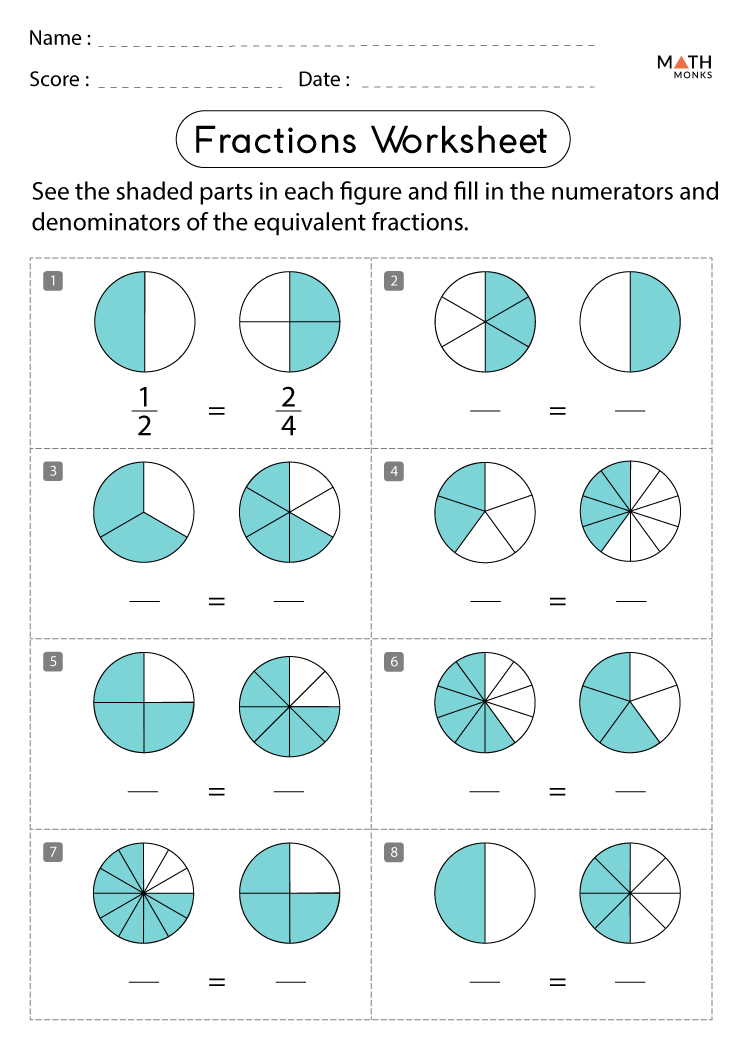
Math 3 Unit 3 Worksheet 2 Answer Key Revealed

The quest to master mathematics is not for the faint-hearted. Every new unit brings its own challenges and complexities, requiring students to delve deep into abstract concepts and practical applications. The Math 3 Unit 3 curriculum, in particular, can be daunting with its introduction to trigonometry, exponential functions, and logarithmic equations. If you're one of the many students trying to wrap your head around the exercises in Worksheet 2, this guide will shine a light on some of the Answer Key solutions to help clarify the intricacies of this lesson.
Understanding Trigonometry Basics

Trigonometry, often deemed as the backbone of Unit 3, deals with the relationships between angles and the sides of triangles. Here's what you need to know:
- Sine (sin): Ratio of the length of the side opposite the angle to the hypotenuse in a right-angled triangle.
- Cosine (cos): Ratio of the length of the adjacent side to the hypotenuse.
- Tangent (tan): Ratio of the sine to the cosine of an angle, or the opposite side over the adjacent side.
Here is a simple table to help memorize these trigonometric functions:
| Function | Relation |
|---|---|
| Sin | Opposite / Hypotenuse |
| Cos | Adjacent / Hypotenuse |
| Tan | Opposite / Adjacent |
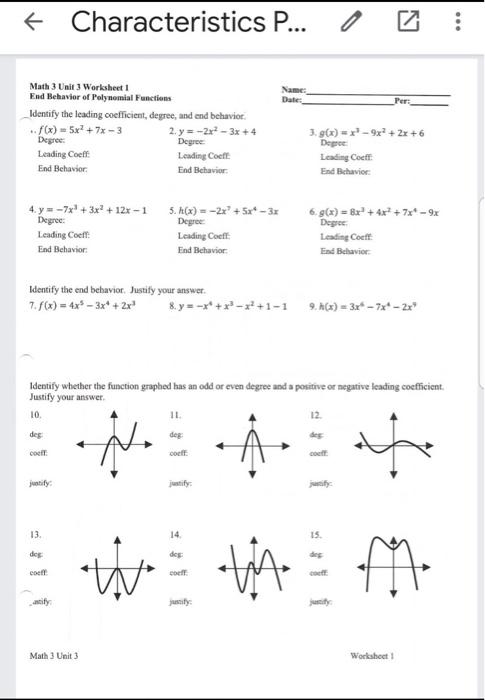
Exploring Exponential and Logarithmic Functions

The introduction of exponential functions and logarithms brings a different layer of complexity to Unit 3. Here's a brief overview:
- Exponential Function: f(x) = a^x where a is the base and must be positive.
- Logarithm: If y = log_b(x), then x = b^y, where b is the base, x > 0, b > 0, b ≠ 1.
Exponential Growth and Decay

Exponential functions can model growth or decay, which is a fascinating aspect to explore. Here are a few pointers:
- When the base a is greater than 1, the function describes exponential growth.
- When 0 < a < 1, the function describes exponential decay.
Logarithmic Relationships

Logarithms are inverses of exponential functions and can be used to solve problems involving time scales:
- Logarithms transform multiplicative relationships into additive ones.
- They can also compress a range of values into a more manageable scale.
Worksheet 2 Answer Key Breakdown

In Math 3 Unit 3 Worksheet 2, you encounter several problems that mix trigonometry with exponential and logarithmic functions. Here’s a walkthrough of some key answers:
Problem 1: Solving Trigonometric Equations

The first few exercises often focus on solving equations like:
- sin(x) = 1⁄2 which has solutions at x = π/6 or x = 5π/6 in a unit circle.
- tan(x) = -1, where x = -π/4 or x = 3π/4.
These problems test your understanding of trigonometric ratios and their inverses.
Problem 2: Working with Logarithms

An example question might be: “Solve log_2(32) = x”. Here’s the step-by-step solution:
- Recognize that log_2(32) means 2^x = 32
- Since 2^5 = 32, x = 5
📌 Note: Always consider the domain and range when dealing with logarithmic functions.
Problem 3: Exponential Equations

Another common question involves exponential equations like “Solve 2^(x+3) = 16”.
- Express 16 as a power of 2; thus, 16 = 2^4.
- Now, equate the exponents: x + 3 = 4, so x = 1.
Problem 4: Using Trigonometric Identities

This problem might ask you to verify an identity like:
- cos^2(x) + sin^2(x) = 1, known as the Pythagorean identity.
- Another identity could be tan(x) = sin(x) / cos(x).
These types of problems help solidify your understanding of how different trigonometric functions relate to each other.
To wrap up, Math 3 Unit 3 Worksheet 2 challenges students to apply their knowledge of trigonometry, exponential functions, and logarithms in varied and often interconnected ways. By dissecting these answers and understanding the underlying principles, students can master these concepts, building a strong foundation for more complex mathematical problems.
What is the significance of trigonometry in real-world applications?

+
Trigonometry is crucial in fields like engineering, astronomy, computer graphics, game design, and navigation. It helps in calculating distances, angles, heights, and waveforms, among other applications.
How can exponential functions be applied outside of the classroom?

+
Exponential functions are used to model population growth, radioactive decay, financial interest, compound growth, and many natural phenomena where growth or decay rates change continuously.
Why are logarithms important in mathematics?

+
Logarithms are used to solve exponential equations, to express very large or small numbers, and in scientific scales like the Richter scale or decibels in sound measurement. They simplify the process of multiplication, division, exponents, and roots through addition and subtraction.