5 Tips for Mastering Linear Inequalities Graphing Worksheet

In the fascinating world of mathematics, linear inequalities are the gateways to understanding how different variables relate in non-strict or strict relationships. While many find equations and graphing linear functions daunting, mastering graphing worksheet for linear inequalities is indeed an achievable feat, especially with the right tools and tips. Here, we delve into five essential tips to help you conquer linear inequalities through graphing worksheets, ensuring you not only understand but also excel in this mathematical domain.
Understanding the Basics

Before you can graph inequalities, you must comprehend what they represent. A linear inequality looks like y < mx + b or y ≤ mx + b and indicates that there’s a set of values for y for which the statement is true, given certain x-values.
- Linear Equation Review: Quickly revise how to graph linear equations to establish a foundation for inequalities.
- Types of Inequalities: Get familiar with "less than" (<), "less than or equal to" (≤), "greater than" (>), and "greater than or equal to" (≥).
📘 Note: Always start with the boundary line which divides the coordinate plane into two regions.
Identify the Boundary Line

To graph a linear inequality, first, you must determine the boundary line, which is the graph of the related linear equation.
- Set inequality to equality: Change the inequality sign to an equal sign to find the boundary line.
- Graph the line: Plot the line based on the equation you've derived.
- Solid or Dashed?: If the inequality is ≥ or ≤, use a solid line. If it's < or >, use a dashed line.
Pick a Test Point

After plotting the boundary line, you need to determine which side of this line represents the solution set for your inequality.
- Choose an easy point: Often (0,0) works well, but you can use any point not on the boundary line.
- Substitute into inequality: Plug the test point into the original inequality. If the resulting statement is true, shade the side containing the test point.
🧮 Note: If the test point makes the inequality true, shade above or to the right of the line for < or ≥, below or to the left for > or ≤.
Shade the Right Region

Once you’ve determined the correct side of the boundary line, the next step is to shade the corresponding region:
- Shading direction: Based on the test point, decide whether to shade above or below the line for vertical shading or to the left or right for horizontal shading.
- Consistent shading: Ensure the shading is consistent throughout your graph to accurately represent the inequality.
| Symbol | Boundary Line | Shading Direction |
|---|---|---|
| < | Dashed | Below or to the left |
| <= | Solid | Below or to the left |
| > | Dashed | Above or to the right |
| >= | Solid | Above or to the right |

Handle Compound Inequalities

Compound inequalities involve multiple inequalities combined using ‘and’ or ‘or’ operations. Here are some tips to manage them:
- Identify boundary lines: For each inequality in the compound, identify and plot the corresponding boundary lines.
- Consider the operations:
- 'And' statements require both inequalities to be true. Therefore, shade the intersection of the regions of the individual inequalities.
- 'Or' statements require at least one inequality to be true, thus shade the union of the regions.
By following these tips, your ability to graph linear inequalities on a worksheet will significantly improve. Remember, practice is key. The more you engage with these problems, the more intuitive the process becomes.
With the knowledge and tips in hand, here's a summary of what you can expect to take away:
- A clear understanding of linear inequalities' basics and how they relate to graphing.
- The process of identifying boundary lines, choosing test points, and shading regions appropriately.
- The capacity to handle more complex, compound inequalities with confidence.
The journey through the realm of linear inequalities is not just about solving equations but understanding the relationship between variables. By mastering these graphing techniques, you're not only improving your mathematical skills but also enhancing your ability to solve real-world problems where variables are not always equal but within a certain range.
Why do some boundary lines appear dashed, while others are solid?

+
The type of line used reflects the nature of the inequality:
- Dashed lines signify strict inequalities (< or >) where the line itself is not part of the solution set.
- Solid lines are used for non-strict inequalities (≤ or ≥) where the line is included in the solution set.
How do I choose a test point for shading?

+
Choose a point that does not lie on the boundary line. The origin (0,0) is convenient because it simplifies substitution, but any other point will work. Ensure it lies outside the line to accurately test which region to shade.
What if my inequality has variables on both sides?
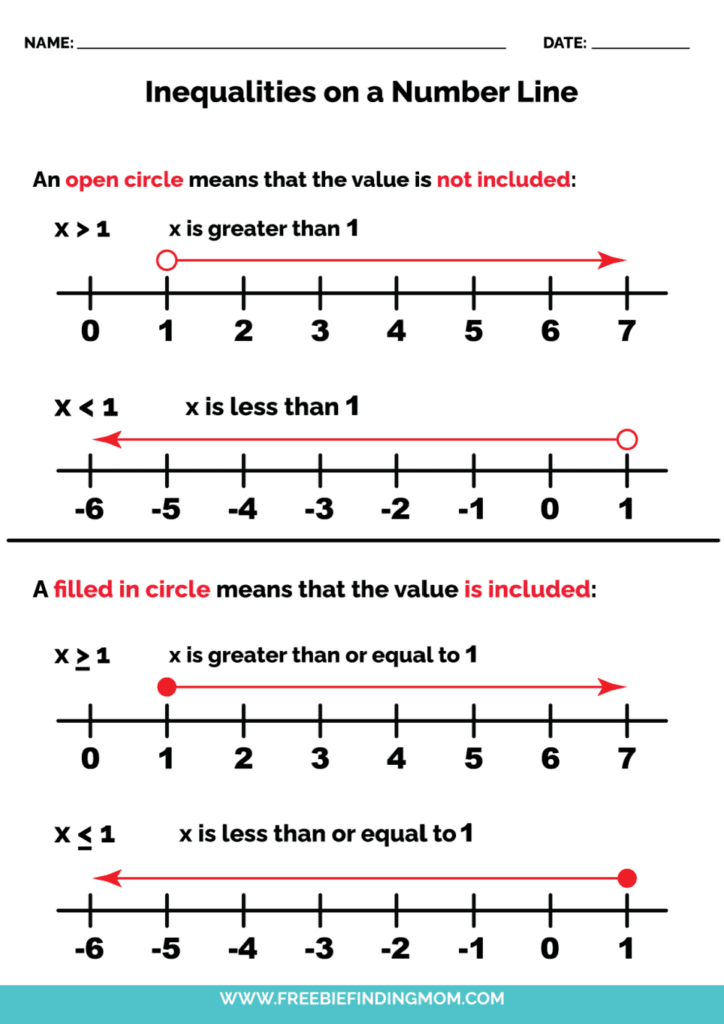
+
Isolate the variable on one side to find the boundary line. For example, if you have 3y - 2x < 6, rearrange to 3y < 2x + 6 or y < (2⁄3)x + 2 to graph the line y = (2⁄3)x + 2.
Can inequalities be represented in a single graph?

+
Yes, you can graph multiple inequalities on the same coordinate plane. Use different shading patterns or colors for different inequalities, or use the intersection/union shading for compound inequalities.



