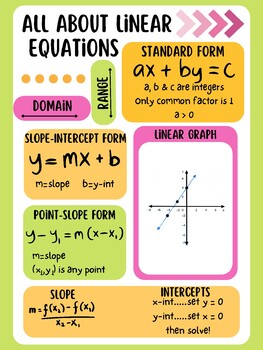
Linear Equations Answer Key: Ultimate Cheat Sheet

Understanding and solving linear equations is a fundamental skill in mathematics. Whether you're a student tackling algebra or an adult brushing up on your math skills, this guide serves as an ultimate cheat sheet for mastering linear equations. In this post, we'll cover key concepts, step-by-step problem-solving strategies, and common pitfalls to avoid. Let's dive into the world of linear equations.
Basics of Linear Equations

A linear equation in its simplest form can be written as:
ax + b = c, whereaandbare constants, andxis the variable we solve for.
Here, a cannot be zero as that would make the equation no longer linear but rather a simple arithmetic problem.
Solving Basic Linear Equations
To solve a basic linear equation:
- Isolate the variable: Move all terms involving
xto one side and constants to the other. Use addition, subtraction, multiplication, or division to achieve this. - Simplify: Perform arithmetic operations in a way that maintains equation balance.
- Solve for
x: Oncexis isolated, perform the final calculation to find its value.
Example:
Given the equation 3x + 5 = 14:
- Subtract 5 from both sides:
3x = 9 - Divide both sides by 3:
x = 3
🔎 Note: Always check your solution by substituting the value back into the original equation to ensure it balances.
Complex Linear Equations

When dealing with more complex equations that have multiple variables or nested terms:
- Distribute and Combine Like Terms: If there are parentheses or brackets, distribute the numbers outside. Combine like terms to simplify the equation.
- Eliminate fractions: Multiply by the least common denominator to get rid of any fractions.
- Step-by-step isolation: Continue isolating the variable as outlined above, but with more steps or intermediate variables.
Example:
Given 2(x - 1) + 3 = 7:
- Distribute 2:
2x - 2 + 3 = 7 - Combine like terms:
2x + 1 = 7 - Subtract 1 from both sides:
2x = 6 - Divide by 2:
x = 3
Linear Equations with Fractions

Handling equations with fractions requires additional care:
- Find the Least Common Denominator (LCD): Identify the LCD of all fractions in the equation.
- Multiply the entire equation by LCD: This eliminates the fractions, allowing for straightforward solving.
Example:
Given (1⁄2)x + (1⁄3) = 1:
- The LCD for 2 and 3 is 6. Multiply the whole equation by 6:
3x + 2 = 6- Subtract 2 from both sides:
3x = 4 - Divide by 3:
x = 4⁄3
🔍 Note: Ensure the algebraic manipulations are done correctly, especially when dealing with negative numbers or variables.
Systems of Linear Equations

When you have more than one linear equation with multiple variables, you can solve them simultaneously. Methods include:
- Substitution: Solve one equation for one variable and substitute that into the other equation(s).
- Elimination (Addition or Subtraction): Adjust the equations to cancel out one variable when added or subtracted together.
Example:
| Equation 1: | 2x + y = 9 |
| Equation 2: | x + y = 6 |

Using substitution:
- From Equation 2:
y = 6 - x - Substitute in Equation 1:
2x + (6 - x) = 9 - Simplify:
x + 6 = 9=>x = 3 - Substitute
xback to findy:y = 6 - 3=>y = 3
By now, you should have a solid grasp of linear equations from basic to complex scenarios. Always remember to verify your solutions, and when dealing with systems, consider multiple methods to find the most efficient solution path. The journey in mastering linear equations is not just about solving problems but understanding the logic and algebra behind the manipulations.
What is the difference between linear and quadratic equations?

+
Linear equations are of the first degree (no term is raised to a power other than 1), while quadratic equations are second degree, with at least one term squared. Solving them involves different techniques, with quadratic equations requiring methods like factoring or the quadratic formula.
Can a linear equation have multiple solutions?

+
No, a single linear equation typically has exactly one solution unless it’s an identity equation (where all terms are effectively zero, giving an infinite number of solutions) or has no solution due to a contradiction.
How do I know if my solution to a linear equation is correct?

+
Substitute your solution back into the original equation. If both sides of the equation balance, your solution is correct. Ensure you perform all algebraic operations correctly during the solving process to avoid mistakes.