Limit Superior and Inferior Explained

Introduction to Limit Superior and Limit Inferior

The concepts of limit superior and limit inferior are fundamental in real analysis, playing crucial roles in understanding the behavior of sequences and functions. These concepts help in determining the bounds within which a sequence or a function operates, especially when dealing with convergence or divergence. In this explanation, we will delve into the definitions, examples, and significance of limit superior and limit inferior, highlighting their importance in mathematical analysis.

Definition of Limit Superior

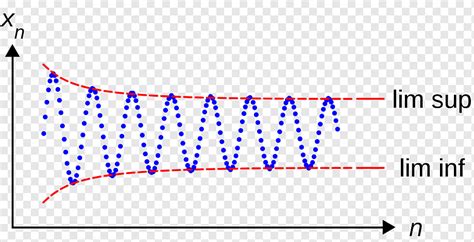
The limit superior of a sequence, denoted as lim sup, is the largest possible limit of subsequences of the given sequence. It represents the supremum of the set of all subsequential limits of the sequence. Mathematically, for a sequence {x_n}, lim sup x_n is the largest real number that is less than or equal to all the subsequential limits of {x_n}. This concept is crucial for understanding how a sequence behaves in the long run, especially when it does not converge.

Definition of Limit Inferior

Conversely, the limit inferior, denoted as lim inf, is the smallest possible limit of subsequences of a given sequence. It represents the infimum of the set of all subsequential limits of the sequence. For the sequence {x_n}, lim inf x_n is the smallest real number that is greater than or equal to all the subsequential limits of {x_n}. The limit inferior provides insight into the lower bound of the sequence’s behavior over time.

Examples and Illustrations

To understand these concepts better, let’s consider an example. Suppose we have a sequence {x_n} defined as x_n = (-1)^n. This sequence oscillates between -1 and 1. The subsequential limits of this sequence are -1 and 1 because we can extract subsequences that converge to either of these values. Therefore, the limit superior of this sequence is 1 (the larger of the two limits), and the limit inferior is -1 (the smaller of the two limits).

Significance in Mathematical Analysis

The concepts of limit superior and limit inferior are significant in various areas of mathematical analysis: - Convergence Tests: These limits help in determining whether a sequence converges or diverges. If the limit superior and limit inferior of a sequence are equal, then the sequence converges to that value. - Boundedness: Limit superior and limit inferior can be used to determine if a sequence is bounded above or below. - Function Analysis: These concepts extend to functions, helping in the analysis of their behavior, especially in the context of continuity and differentiability.

Comparison and Relationship

The limit superior and limit inferior are related but distinct concepts. They provide upper and lower bounds, respectively, for the behavior of sequences or functions. Understanding their relationship is crucial for analyzing complex sequences and functions. The limit superior is always greater than or equal to the limit inferior. When these two values are equal, it signifies the convergence of the sequence or function to a single limit.

📝 Note: The limit superior and limit inferior can also be applied to sets, where they help in understanding the supremum and infimum of the set in the context of limit points.

Applications in Real-World Scenarios

These concepts have practical applications in: - Economics: For analyzing economic trends and predicting future behaviors of economic indicators. - Signal Processing: In filtering signals and understanding the boundedness of signal sequences. - Computer Science: In algorithm analysis, where understanding the bounds of sequences can help in predicting algorithmic complexity.

Conclusion Summary

In summary, limit superior and limit inferior are foundational concepts in real analysis, offering insights into the behavior of sequences and functions. They provide a framework for understanding convergence, boundedness, and the long-term behavior of mathematical objects. By grasping these concepts, one can better analyze and predict the behavior of complex systems in various fields, from economics to computer science.