Master Exponents with Free Laws of Exponents Worksheets

In mathematics, the concept of exponents plays a fundamental role in simplifying expressions and solving various problems. Exponents, or powers, are numerical notations that indicate how many times a base number is multiplied by itself. Understanding the laws of exponents is crucial for anyone looking to excel in algebra, calculus, or any advanced math. This comprehensive guide will walk you through the laws of exponents, provide practical examples, and give you access to free laws of exponents worksheets to reinforce your understanding.
Understanding Exponents

An exponent signifies the number of times you multiply a number (the base) by itself. For instance, in the expression 23, 2 is the base, and 3 is the exponent. Here, 2 is multiplied by itself 3 times:
- 23 = 2 × 2 × 2 = 8
Laws of Exponents
There are several fundamental rules or laws that govern how exponents interact with one another:
1. Product Rule

When multiplying two exponential expressions with the same base, you add the exponents:
am × an = am+n
For example, 52 × 53 = 52+3 = 55 = 3125.
2. Quotient Rule

When dividing two exponential expressions with the same base, you subtract the exponents:
am ÷ an = am-n
As an example, 48 ÷ 45 = 48-5 = 43 = 64.
3. Power Rule

When raising an exponential expression to another power, you multiply the exponents:
(am)n = am×n
Here’s an example: (62)3 = 62×3 = 66 = 46656.
4. Zero Rule

Any non-zero number raised to the power of zero equals 1:
a0 = 1
Thus, 30 = 1.
5. Negative Exponent Rule

A negative exponent means you take the reciprocal of the base and make the exponent positive:
a-n = 1/an
For instance, 2-3 = 1⁄23 = 1⁄8.
6. Fractional Exponent Rule
A fractional exponent indicates taking the root (the denominator) of the base and raising it to the numerator:
a(m/n) = (n√a)m or √an
For example, 8(2⁄3) = (³√8)2 = 22 = 4.
Why are Exponents Important?

Exponents are more than just a mathematical abstraction; they are essential in:
- Calculating growth and decay in science and economics like exponential growth models, compound interest, and radioactive decay.
- Simplifying expressions and equations in algebra.
- Measuring scales and units in technology and engineering.
- Computer science for algorithms and data structures.
- Statistics and probability for power laws.
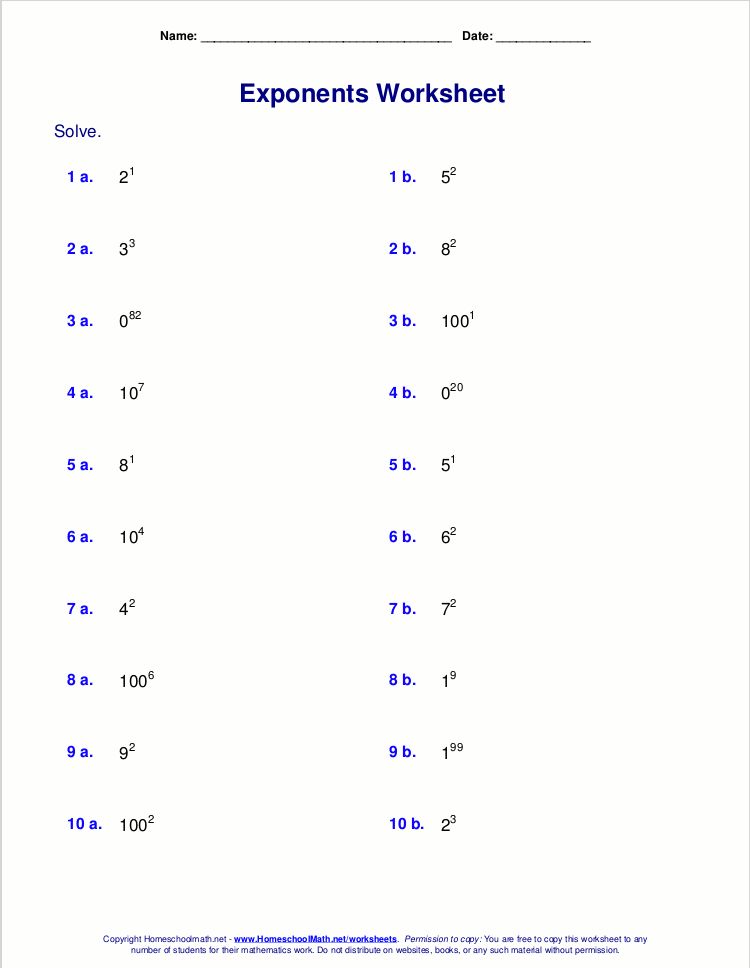
Worksheets to Enhance Understanding

To reinforce your understanding of exponents, we have curated free downloadable worksheets:
| Worksheet | Description |
|---|---|
| Exponent Basics | Practice with the fundamental rules of exponents. |
| Advanced Exponent Rules | Work through complex problems involving the power rule, negative exponents, and fractional exponents. |
| Exponent Simplification | Master simplifying expressions using multiple exponent rules. |

These worksheets are invaluable tools for students and educators, providing:
- Step-by-step solutions to guide learning.
- A mix of problems catering to different learning paces.
- Real-world applications to show the practical use of exponents.
Each worksheet includes detailed instructions, making it easier for users to understand the problems:
- Basic Problems: Simplify straightforward expressions like 22 + 33 using the laws of exponents.
- Complex Problems: Solve problems involving negative exponents or fractional exponents, such as simplifying (4-1) + (91/2).
- Mixed Operations: Use all rules of exponents in a single expression, like simplifying (81/3)4 × (4-2) + 20.
Exponent Practice Tips

Here are some tips to effectively practice with these worksheets:
- Start with basic laws before moving to more complex rules.
- Write down the steps to see how different laws interact in one problem.
- Use visual aids or diagrams to understand the exponent rules better.
📌 Note: Practice is the key to mastering exponents. Regularly working through worksheets will not only improve your understanding but also increase your speed and accuracy in dealing with exponents.
In Summary

Exponents are fundamental in mathematics, providing a concise way to handle repeated multiplication. Through a thorough understanding of the laws of exponents, you can simplify expressions, solve complex problems, and apply this knowledge to real-world scenarios. The worksheets provided serve as excellent practice material, ensuring that you can master these laws through repetition and real-world examples. Remember, consistency and practice are your best allies in mastering exponents, so keep working at it, and you’ll find exponents becoming an intuitive part of your mathematical toolkit.
What are exponents used for in real life?

+
Exponents are utilized in various fields like finance for compound interest, population growth models, physics for measuring power, and computer science for data compression and algorithms.
How do I memorize the laws of exponents?

+
It’s helpful to use mnemonic devices, create flashcards, and practice problems regularly. Visualizing the laws with examples can also aid memory retention.
Why are there different rules for negative exponents?

+
Negative exponents represent the reciprocal of the base to make exponent notation consistent across different numbers and simplify calculations involving division.