5 Law of Sines Worksheet Tips for Geometry Success

Many students grapple with the complexities of trigonometry, but mastering the Law of Sines can unlock a plethora of geometric problems. This vital tool is indispensable for tackling triangle-related challenges, making it a cornerstone of geometry success. Here, we'll delve into five strategic tips to help you better understand, apply, and leverage the Law of Sines in your geometry studies and problem-solving efforts.
The Importance of Understanding the Basics


Before you dive into the application of the Law of Sines, you must ensure you have a solid grasp of its foundation. The Law of Sines states:
a / sin(A) = b / sin(B) = c / sin©
Where a, b, c are the lengths of the sides of a triangle, and A, B, C are the angles opposite those sides. Understanding this equation is paramount as it connects the triangles’ sides with their opposite angles in a harmonic relationship.
Utilize Diagrams to Your Advantage
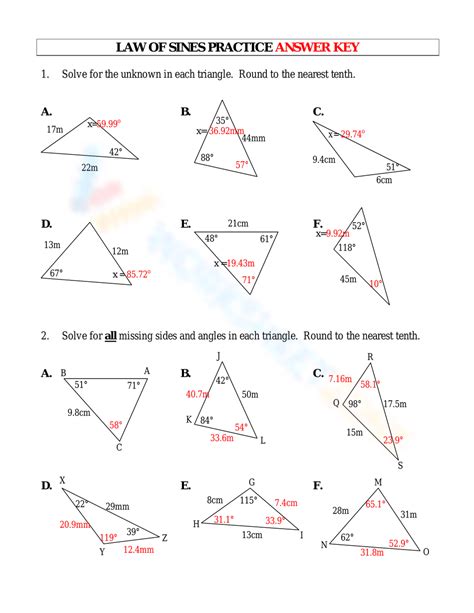
Visual representation of the problem can greatly enhance your ability to solve using the Law of Sines. Here’s how you can use diagrams effectively:
- Draw a clear, labeled diagram of the triangle.
- Identify which pieces of information you have and which you need to find.
- Label the angles and sides with their known measurements.
- Use different colors to distinguish between known and unknown values.
Practice with Various Problems

Like many mathematical concepts, practice is key to mastering the Law of Sines. Here are different types of problems to tackle:
- Problems with two sides and a non-included angle given.
- Problems where you have to find an angle given three sides (SSA condition).
- Solving ambiguous case scenarios.
- Real-world applications like navigation or surveying problems.
⚠️ Note: Be mindful of the ambiguous case, where there can be two solutions for the angle if the given side is longer than the other known side but shorter than the sum of the other side and the opposite angle.
Understand the Angle Relationships

The Law of Sines is not just about numbers; it’s about understanding the spatial relationships between angles:
- The sum of angles in a triangle is 180°.
- The largest angle is opposite the longest side.
- Angles can be found using supplementary angles in isosceles or right triangles.
Use Technology and Tools

In today’s digital age, leveraging technology can provide an extra boost:
- Use geometry software or apps to explore triangle configurations.
- Graphing calculators or online tools can help verify your calculations.
- There are many online resources like video tutorials, interactive exercises, and forums for additional help.
💡 Note: While technology aids in practice, ensure you understand the concepts manually first to foster deeper learning.
Mastering the Law of Sines opens up a world of possibilities in geometry, from simple problem-solving to tackling more complex real-world scenarios. By grounding yourself in the basic principles, using visual aids, practicing widely, understanding angle relationships, and utilizing technology, you'll elevate your geometry game. In this journey, remember that patience, practice, and persistent application of these tips will ensure you unlock the full potential of this geometric theorem.
What is the main purpose of the Law of Sines?

+
The Law of Sines helps solve triangles when you know certain combinations of sides and angles, particularly in non-right angled triangles.
Can the Law of Sines be applied to all triangles?

+
Yes, the Law of Sines applies to all triangles, including acute, right, and obtuse triangles.
What is the “ambiguous case” in the Law of Sines?

+
The ambiguous case arises when the given information (SSA) might not uniquely define the triangle, leading to the possibility of having two solutions for one of the angles.
How does the Law of Sines differ from the Law of Cosines?

+
While the Law of Sines deals with angles and their opposite sides, the Law of Cosines is used to find a side or angle when you know two sides and the included angle or all three sides of a triangle.
Are there any real-world applications of the Law of Sines?
+
Yes, the Law of Sines is used in navigation, surveying, engineering, physics, and astronomy for solving problems involving distance, angles, and positioning.