5 Law of Sines and Cosines Word Problems Solved

The Law of Sines and Cosines are fundamental principles in trigonometry that are particularly useful when solving for sides or angles in non-right triangles. These laws are not only theoretical constructs but are also applied in various real-world scenarios, from navigation to architecture. In this post, we will explore how these laws can be used to solve practical problems, making their application clear and accessible.
The Law of Sines

The Law of Sines states that in any triangle, the ratio of the length of a side to the sine of the opposite angle is the same for all three sides. It can be expressed as:
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\]
- a, b, c are the sides opposite to angles A, B, and C respectively.
📚 Note: This law is particularly useful when you know two angles and a non-included side or when two sides and an angle opposite one of these sides are known.
Problem 1: The Tower Angle Problem

Scenario: From the base of a tower, the angle of elevation to the top is 45 degrees. Walking 50 meters from the tower, the angle of elevation becomes 30 degrees. Find the height of the tower.
| Given Data: | Angle of Elevation from Base (θ₁) = 45° | Angle of Elevation after Walking (θ₂) = 30° | Distance Walked (d) = 50 meters |

Solution:
- Label the sides and angles according to the tower setup. Let the height of the tower be h and the base angle be A = 45°.
- Using the Law of Sines, we can write:
h/sin(45°) = 50/sin(15°)
- Since sin(45°) = 1/√2 and sin(15°) ≈ 0.259, we find:
h = 50 * (1/√2 / 0.259) ≈ 113.6 meters
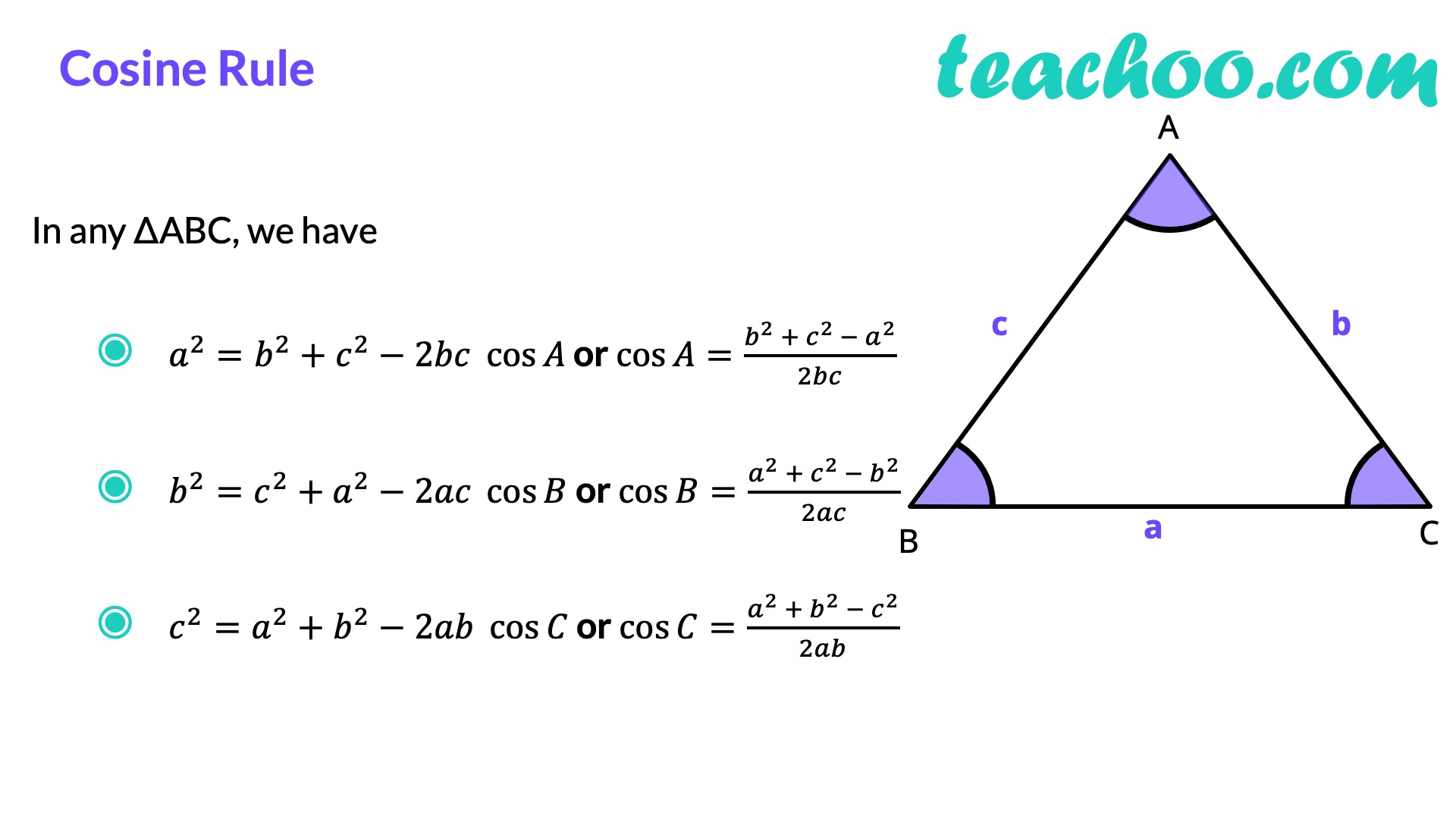
The Law of Cosines

When the angles of a triangle are not known but all sides or some sides and one angle are given, the Law of Cosines comes into play. It states:
\[a^2 = b^2 + c^2 - 2bc \cos A\]
- Here, a is the side opposite angle A, and b and c are the other two sides.
Problem 2: The Surveyor’s Dilemma

Scenario: A surveyor needs to determine the distance between two points, A and B, on opposite sides of a lake. He can measure the following:
| AB = Distance between A and B (unknown) |
| AC = 800 meters |
| BC = 750 meters |
| ∠C = 100 degrees |
Solution:
- Using the Law of Cosines to solve for AB:
AB² = 800² + 750² - 2 * 800 * 750 * cos(100°)
- cos(100°) ≈ -0.1736, giving us:
AB² ≈ 800² + 750² + 2 * 800 * 750 * 0.1736
- Calculating, AB ≈ 714.1 meters
🚫 Note: The angle must be between 0° and 180° when using the Law of Cosines.
Problem 3: Airplane Navigation

Scenario: An airplane flies from point X to Y due east, then changes course by flying northeast to point Z. Given the distances and bearings, calculate the total distance traveled.
| Distance XY = 200 km |
| Distance YZ = 150 km |
| Bearing XY = 90° (due east) |
| Bearing XZ = 45° (northeast) |
Solution:
- Since we need to find the total distance from X to Z through Y, we can use the Law of Cosines:
- The angle at Y between XY and YZ is 90° - 45° = 45°:
XZ² = 200² + 150² - 2 * 200 * 150 * cos(45°)
- cos(45°) = 1/√2, so:
XZ ≈ 239.1 km
Recap and Summary

We've explored several practical applications of the Law of Sines and Cosines. From calculating the height of towers to determining distances across lakes and navigational paths, these trigonometric laws are indispensable for engineers, surveyors, and anyone who works with non-right triangles. They provide an elegant solution to what would otherwise be complex geometric problems, allowing us to measure distances or angles that are not directly observable or measureable.
Can the Law of Sines or Cosines be used for right triangles?
+
Yes, for right triangles, the Law of Sines is not needed as the Law of Cosines reduces to the Pythagorean theorem when one of the angles is 90 degrees.
How do you decide which law to use when given different information about a triangle?

+
Use the Law of Sines if you have at least two angles and one side or two sides and one angle opposite to one of the sides. Use the Law of Cosines for SSS (three sides) or SAS (two sides and included angle).
What if I have an ambiguous case with the Law of Sines?

+
The ambiguous case refers to situations where given two sides and an angle, there might be two possible triangles (or even none). To resolve this, additional information or geometric analysis is necessary.