5 Tricks to Solve Ambiguous Case in Law of Sines

Let's delve into an essential trigonometric concept that can sometimes confuse even the brightest math students: the ambiguous case in the Law of Sines. This case arises in scenarios where you have two sides and an angle that isn't included between them, often leading to multiple possible triangles. Here are five tricks to navigate and solve this tricky situation effectively.
1. Understand What Makes the Ambiguous Case

Before diving into the solutions, understanding the root of the ambiguity is crucial:
- You have two sides and an angle that isn’t included between them, typically labeled as (a), (b), and (A) respectively.
- This setup can lead to multiple possible triangles because there are generally two angles (C) where ( \sin© = \frac{a \cdot \sin(A)}{b} ).
- The ambiguity comes from the fact that the sine function is positive in both the first and second quadrants.
💡 Note: The Law of Sines is given by (\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}).
2. Use the Sinusoidal Ambiguity Rule

The sinusoidal ambiguity rule helps identify how many triangles can be formed:
- If ( a \leq b \sin(A) ), no triangle exists.
- If ( a = b \sin(A) ), one unique triangle exists, where ( \angle B = 90 - A ).
- If ( b \sin(A) < a < b ), two non-congruent triangles exist.
- If ( a \geq b ), one or two triangles exist depending on further conditions.
| Condition | Number of Triangles |
|---|---|
| (a \leq b \sin(A)) | 0 |
| (a = b \sin(A)) | 1 |
| (b \sin(A) < a < b) | 2 |
| (a \geq b) | 1 or 2 |
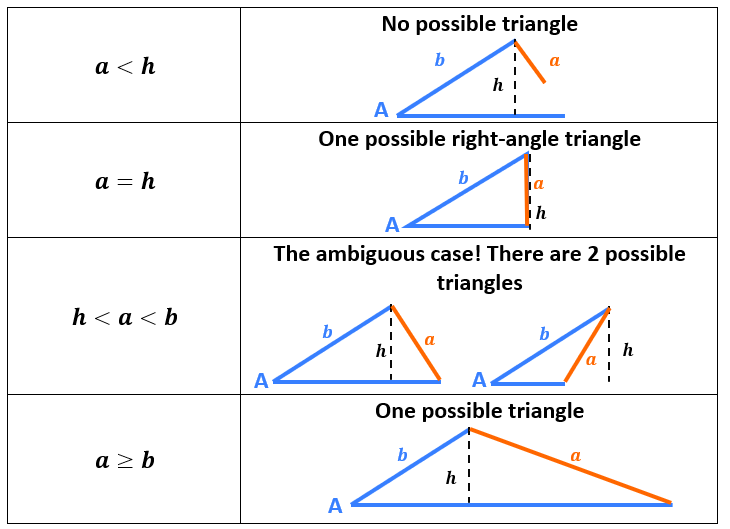
3. Calculate the Height of the Triangle

Visualizing the problem can often help:
- Draw side (a) as the base.
- Calculate the height from (a) to the opposite vertex using the sine rule: (h = b \sin(A)).
- If (h) exceeds the length of (a), no triangle can be formed.
- If (h = a), then ( \angle B = 90 - A ).
- If (h < a), visualize two different triangles where the height intersects the base.
4. Apply the Law of Cosines as a Check

Using the Law of Cosines after applying the Law of Sines can help in cross-verifying solutions:
- If you solve for (B) with the Law of Sines, use the Law of Cosines to find (c) and verify (c^2 = a^2 + b^2 - 2ab \cos(B)).
- Check if the results from both methods align. If not, you might have to discard or adjust your solution.
🧐 Note: The Law of Cosines states (c^2 = a^2 + b^2 - 2ab \cos(\gamma)).
5. Consider Both Angles

When two triangles are possible, consider both angles (B) and (B’):
- One angle (B) is found using the sine rule: (B = \sin^{-1}\left(\frac{a \cdot \sin(A)}{b}\right)).
- The other angle (B’) is given by (B’ = 180 - B).
- Calculate the corresponding angles (C) for both (B) and (B’), and find side (c) in both cases using the Law of Sines.
- Make sure both triangles are feasible by checking all angles sum up to (180^\circ).
To wrap things up, understanding the ambiguous case in the Law of Sines is crucial for anyone dealing with triangle trigonometry. By mastering these five tricks—understanding the rules, calculating heights, cross-verifying with the Law of Cosines, and considering both angles—you'll be well-equipped to solve these ambiguous problems. Keep in mind the importance of accurate geometric visualization and rigorous mathematical checks to ensure your solutions are not just correct but also insightful.
Why is there an ambiguous case in the Law of Sines?

+
The Law of Sines uses the sine function, which has the property of being positive in both the first and second quadrants, leading to the possibility of two different angles having the same sine value, thus creating ambiguity in triangle solutions.
Can more than two triangles exist in the ambiguous case?

+
No, due to the triangle inequality theorem and the properties of the Law of Sines, only up to two non-congruent triangles can exist in the ambiguous case scenario.
What should you do if neither solution seems to work?

+
If neither solution from the Law of Sines fits the triangle criteria or leads to valid angles, it might indicate a calculation error or that the given values are incompatible with triangle formation. Double-check your work and consider using alternative methods like the Law of Cosines for verification.