Master the Law of Cosines with Our Practice Worksheet

If you've been on a quest to master trigonometry, you'll find that the Law of Cosines is a pivotal concept. Whether you're gearing up for an exam or just trying to sharpen your geometric skills, understanding and applying the Law of Cosines effectively can greatly enhance your grasp of spatial relationships and measurements. This comprehensive guide will walk you through the intricacies of the Law of Cosines with a practice worksheet to cement your understanding.
What is the Law of Cosines?

The Law of Cosines is an extension of the Pythagorean theorem, applied to any triangle, not just right-angled ones. It's particularly useful for finding unknown sides or angles in triangles where you might not have right angles or when using the Pythagorean theorem isn't applicable. Here's the formula:
c2 = a2 + b2 - 2ab cos(C)
- a, b, c: The sides of the triangle
- C: The angle opposite side c
When to Use the Law of Cosines

The Law of Cosines becomes your go-to tool in the following scenarios:
- Solving Triangles: When you have three sides and need to find angles (SAS configuration) or when you have two sides and the included angle (ASA configuration) to find the remaining sides or angles.
- Non-Right Triangles: Especially useful when dealing with triangles that aren't right-angled.
- Ambiguous Case: The law helps resolve situations where the triangle's configuration could have multiple solutions.
Steps to Solve Problems Using the Law of Cosines

Here's how you can approach problems involving the Law of Cosines:
- Identify the Triangle: Make sure you have the required information, typically two sides and the angle between them or all three sides.
- Apply the Formula: Use the Law of Cosines to find the side or angle you need.
- Solve for Unknown: Whether it's an angle or a side, rearrange the formula to solve for the unknown. Remember, for angles, you'll need the inverse cosine function.
- Check Your Work: Ensure your solution is reasonable and fits within the possible range (angles 0° to 180°, sides positive).
📚 Note: Always check if you're solving for an angle or a side, as the steps to solve will differ.
Practice Worksheet for the Law of Cosines
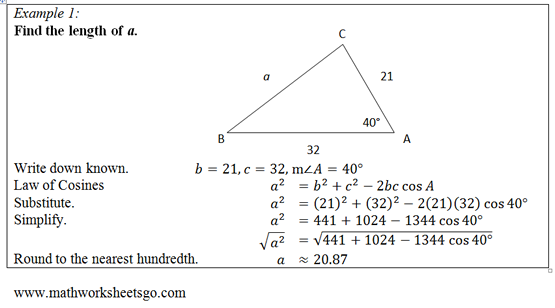
Here are some exercises to practice applying the Law of Cosines:
| Problem | Solution |
|---|---|
| 1. Given sides a = 6 cm, b = 8 cm, and angle C = 60°, find side c. | c2 = a2 + b2 - 2ab cos(C) c = √(62 + 82 - 2*6*8*cos(60)) c ≈ 6.93 cm |
| 2. In a triangle, the sides are a = 5 cm, b = 7 cm, and c = 10 cm. Find angle A. | cos(A) = (b2 + c2 - a2) / (2bc) A ≈ 35.26° |

📝 Note: Ensure your calculator is set to degrees or radians as per the question's requirement.
Tips for Success

- Understand the Concept: Don't just memorize the formula; understand why it works. This understanding will help in applying it more effectively.
- Practice: Like any skill, the more you practice, the more proficient you'll become. Solve different types of problems to get comfortable with all aspects of the Law of Cosines.
- Verify Your Results: Always verify your answers, especially when dealing with angles, to ensure they fall within the correct range.
In summary, mastering the Law of Cosines enhances your ability to solve a wide range of geometric problems, especially in the realm of non-right triangles. By following these steps, practicing with worksheets, and internalizing the concept, you'll find yourself not just solving problems but truly understanding the geometry behind the numbers.
Can the Law of Cosines be used for any triangle?

+
Yes, the Law of Cosines can be applied to any triangle, regardless of whether it is right-angled, obtuse, or acute.
Why isn’t the Pythagorean theorem sufficient?

+
The Pythagorean theorem only applies to right-angled triangles. For triangles without a right angle, you need the Law of Cosines to account for the influence of the angle on the lengths of the sides.
What if I forget the formula during an exam?

+
Understanding the concept helps; however, it’s good practice to memorize the formula. Additionally, some exams provide formulas, so check the rules or use the provided resources if available.