Kepler's Laws Worksheet Answers: Unlocking Orbital Secrets
The study of celestial bodies and their motions has fascinated humanity since time immemorial. Johannes Kepler, a pivotal figure in astronomy, formulated three laws that revolutionized our understanding of planetary movement. Kepler's Laws govern the motions of planets, satellites, and comets, providing the mathematical and observational foundation for our comprehension of the solar system and beyond. Here, we delve into these laws, exploring their implications, historical context, and practical applications through worksheet answers designed to enhance your understanding.
The Historical Context of Kepler's Laws

Before diving into the specifics of Kepler's Laws, it's essential to understand their historical significance. Born in 1571, Johannes Kepler was influenced by the Copernican revolution, which posited that the sun, not the Earth, was the center of the solar system. Kepler, however, improved upon this model, recognizing that the planets did not move in perfect circles but in ellipses, leading to his groundbreaking contributions:
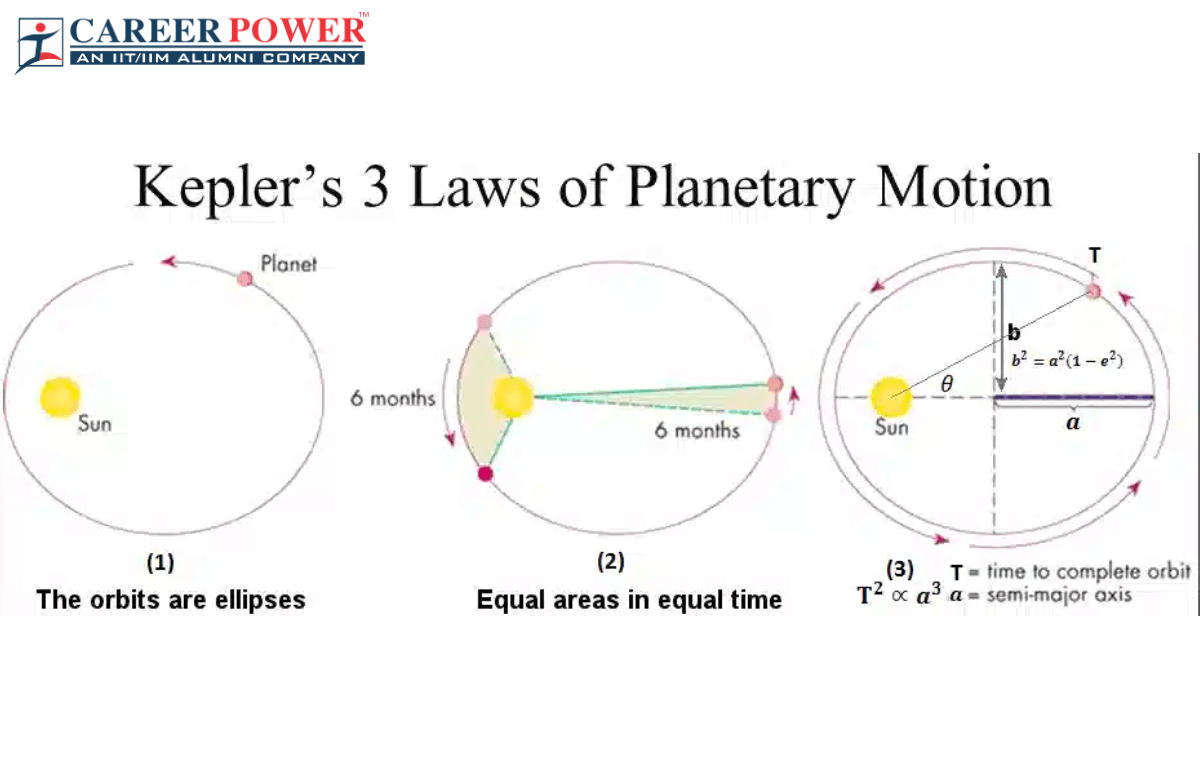
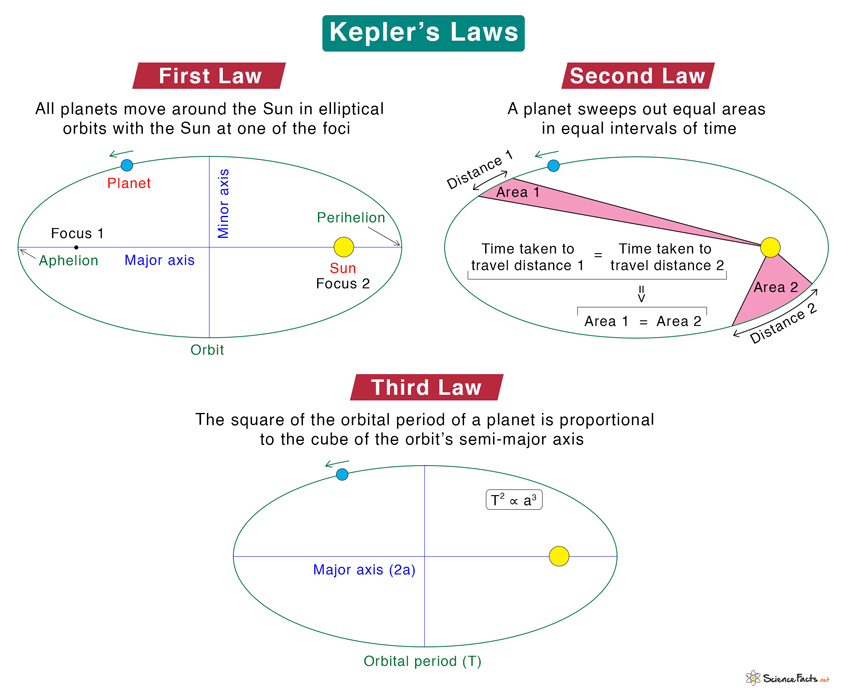
- The Law of Orbits (First Law): Planets move in elliptical orbits with the Sun at one focus.
- The Law of Areas (Second Law): A line connecting a planet to the Sun sweeps out equal areas in equal times.
- The Law of Periods (Third Law): The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.
🌌 Note: Kepler's work was a significant departure from the circular orbit model, which made his laws revolutionary for their time.
Kepler's First Law: The Law of Orbits

Kepler's First Law challenges the then-prevailing idea that planets travel in perfect circles:
- An ellipse has two foci, and the Sun is at one of these foci.
- The eccentricity (e) of the orbit, which measures how much an ellipse deviates from being a circle, ranges from 0 (a perfect circle) to 1 (a line).

Worksheet Answer:

| Question | Answer |
|---|---|
| What shape do planetary orbits follow according to Kepler? | Planets move in elliptical orbits. |
| Where is the Sun located in these orbits? | The Sun is located at one of the two foci of the ellipse. |

Kepler's Second Law: The Law of Areas

This law describes how a planet moves in its orbit:
- Imagine a line connecting a planet to the Sun. As the planet orbits, this line sweeps out areas in the ellipse.
- Equal areas are covered in equal times, meaning a planet moves faster when closer to the Sun (perihelion) and slower when farther away (aphelion).

Worksheet Answer:

| Question | Answer |
|---|---|
| What does Kepler's Second Law state about the motion of a planet? | A line joining the planet to the Sun sweeps out equal areas in equal times. |
Kepler's Third Law: The Law of Periods

Kepler's Third Law offers a relationship between the time it takes a planet to complete an orbit (the orbital period) and the size of the orbit (the semi-major axis):
- P² = a³, where P is the orbital period in years, and a is the semi-major axis in astronomical units (AU).
- This law connects the dynamics of planets in our solar system and can be applied to any two-body gravitational system.

Worksheet Answer:

| Question | Answer |
|---|---|
| What is the relationship between a planet’s orbital period and its semi-major axis? | The square of the orbital period is directly proportional to the cube of the semi-major axis (P² = a³). |
Practical Applications of Kepler's Laws
Kepler's Laws are not just abstract mathematical formulas; they have direct applications in:
- Satellite Orbits: They allow engineers to predict and design satellite trajectories accurately.
- Astronomy: These laws help in discovering exoplanets by analyzing the light curves of stars.
- Space Travel: Mission planners use Keplerian orbits to calculate transfer orbits between planets.
- GPS Navigation: The precision of GPS signals relies on an understanding of how objects orbit the Earth.
🚀 Note: Kepler's Laws serve as the foundation for modern space exploration, offering predictability to celestial mechanics.
Education and Teaching Kepler's Laws

Teaching Kepler's Laws can be engaging through:
- Visual Models: Creating or using planetariums, interactive software, or 3D models to illustrate elliptical orbits.
- Simulations: Using computer simulations to demonstrate the sweep of areas and the proportional relationship of periods.
- Real-Life Examples: Discussing how NASA uses these laws in planning space missions or analyzing data from telescopes like Hubble.
Worksheet Examples

Here are some common questions that might appear on a Kepler's Laws worksheet:
| Question | Answer |
|---|---|
| If Mars has an orbital period of 1.88 years, what is the length of its semi-major axis in AU? | Using Kepler's Third Law, (1.88)² = a³, solving for a, we get a ≈ 1.52 AU. |
| How does a planet's speed change as it moves closer to or farther from the Sun? | According to Kepler's Second Law, a planet will move faster when it is closer to the Sun due to the conservation of angular momentum. |
These worksheets and answers can help students grasp how Kepler's Laws apply not only in theoretical contexts but also in practical scenarios like the planning of space missions.
In Summary

Understanding Kepler's Laws has taken us from the observational astronomy of past centuries to the precise calculations of celestial mechanics in the present. These laws have not only deepened our knowledge of our cosmic neighborhood but have also laid the groundwork for technologies we rely on daily. From predicting eclipses to navigating across vast distances, Kepler's work has left an indelible mark on our understanding of the universe. His dedication to reconciling observations with mathematical precision provides an enduring legacy that continues to inspire and inform astronomers and laypeople alike.
How did Kepler come to formulate these laws?

+
Kepler inherited the meticulous observations of his predecessor, Tycho Brahe. He used Brahe’s data to deduce that planets move in ellipses, formulating his first law. The laws were derived through years of painstaking calculation and pattern recognition, reflecting Kepler’s deep commitment to aligning observations with mathematical theory.
Are Kepler’s Laws still relevant today?

+
Yes, Kepler’s Laws remain foundational for understanding planetary motion, satellite orbits, and are essential in calculating the orbits of bodies in space. They are adapted and expanded upon by modern laws of gravitation and orbital mechanics.
Can Kepler’s Third Law be used for any object orbiting another?

+
Yes, Kepler’s Third Law can be applied to any two-body gravitational system, not just planets orbiting the Sun. This includes moons orbiting planets, satellites around Earth, and even binary star systems.