5 Ways to Master Irrational Numbers Easily

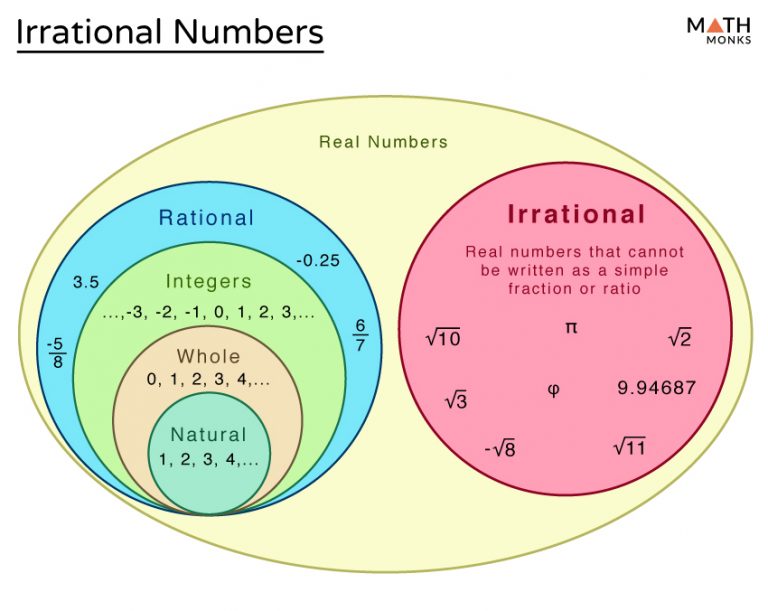
When we delve into the world of mathematics, especially arithmetic, numbers can be classified in numerous ways. One fascinating and sometimes perplexing category is irrational numbers. These are real numbers that cannot be expressed as a simple fraction or ratio of two integers. If you're interested in gaining mastery over irrational numbers, here are five proven strategies to make learning and understanding them much easier.
1. Understand the Concept Through Examples

Begin by familiarizing yourself with common irrational numbers like π (pi), e (Euler’s number), and √2 (square root of 2). Knowing these will not only help in understanding what makes a number irrational but also give you a tangible reference point:
- Pi (π): It’s approximately 3.14159 and continues infinitely without repeating.
- Euler’s number (e): About 2.71828, its decimal representation is non-repeating and non-terminating.
- Square Root of 2 (√2): This is approximately 1.414213, and like π and e, it continues without terminating or repeating.
Use Visual Aids

Incorporate visual aids to understand these numbers better:

2. Practice Decimal Representation

One effective way to master irrational numbers is by exploring their decimal forms. Here’s how:
- Use a calculator or software to generate the first 100 decimal places of π, e, or √2. This gives you a sense of their non-repeating nature.
- Experiment with algebraic equations and use tools to approximate irrational numbers, which helps solidify the concept of their infinite, non-repeating decimal representation.
🔍 Note: While calculators can provide approximations, be aware that these tools might round values, which can slightly alter the actual number.
3. Apply Irrational Numbers in Geometry and Calculus
Irrational numbers play a crucial role in both geometry and calculus:
- Geometry: π is essential in calculating the circumference and area of circles. You can explore problems involving circles, arcs, and sectors.
- Calculus: Euler’s number, e, is fundamental in exponential growth, logarithms, and natural logarithms. Engaging with calculus problems involving e can demystify its significance.
Real-World Application

Relate irrational numbers to real-world scenarios:
| Irrational Number | Application |
|---|---|
| π (pi) | Area calculations for round objects like pizzas or wheels. |
| e (Euler’s number) | Compound interest calculation in banking. |

4. Use Proofs and Properties

Engage with proofs that show why certain numbers are irrational:
- Look into proofs of the irrationality of √2, where an assumption that √2 is rational leads to a contradiction.
- Understand the properties of irrational numbers, such as their density among the reals, and how they interact with rational numbers (addition, multiplication).
5. Embrace Continuous Learning

Mathematics, especially at this level, is a journey, not a destination. Here are strategies for continuous engagement:
- Regular Practice: Keep practicing irrational number calculations, even if they are basic, to maintain and reinforce your understanding.
- Explore Advanced Topics: Delve into topics like transcendental numbers (of which π and e are examples) or the continued fractions representation of irrationals.
- Use Interactive Tools: Websites and apps that allow for interactive math exploration can make learning about irrationals more engaging and less abstract.
Throughout your journey in mastering irrational numbers, you'll find that with each strategy, your familiarity with these seemingly elusive numbers will grow. The process is akin to learning a language; at first, it might seem foreign, but with consistent practice, it becomes second nature. Understanding irrational numbers opens up doors to a more profound appreciation of mathematics and its myriad applications, making you not just a student of numbers, but a master of their nuances.
What makes a number irrational?
+
A number is irrational if it cannot be expressed as a fraction where both the numerator and the denominator are integers. Its decimal form is neither repeating nor terminating.
How can I remember the difference between rational and irrational numbers?

+
Think of ‘rat’ for rational - numbers that can be written as a ratio or fraction, and ‘irrat’ for irrational - numbers that can’t be expressed in this simple form.
Are there any patterns in irrational numbers?

+
While the sequence of digits in irrational numbers is infinite and non-repeating, mathematicians have found some hidden patterns, though they are not easily discernible by simple observation.
Can irrational numbers be negative?

+
Yes, irrational numbers can be both positive and negative. For example, -√2 is irrational just like √2.
Where can I practice working with irrational numbers?

+
Many educational platforms offer math exercises, problems, and interactive tools specifically designed for practicing and mastering irrational numbers. Websites like Khan Academy, Mathway, or WolframAlpha are excellent resources.