Inverse Function Worksheet: Master Solutions and Answers

Understanding Inverse Functions

Functions are one of the foundational concepts in mathematics, and among them, the idea of an inverse function stands as a pinnacle of complexity and utility. An inverse function essentially reverses another function. If a function f maps an element x to y, then the inverse function, f-1, will map y back to x. This concept not only deepens the understanding of functions but also has broad applications in various scientific and engineering disciplines, including solving equations, cryptography, and machine learning.
Why Inverse Functions Matter
Inverse functions are not just a theoretical construct; they are incredibly practical. Here are some reasons why mastering inverse functions can be beneficial:
- Solving Equations: They help solve for unknown variables where the function value is known.
- Optimization Problems: In calculus, knowing the inverse of a function can assist in finding maximum or minimum values.
- Data Encoding: Inverse functions play a crucial role in data compression and encoding algorithms.
- Machine Learning: Understanding the nature of functions and their inverses helps in the design of neural networks.
How to Find Inverse Functions

Finding the inverse of a function involves several steps. Let's break it down:
1. Verify the Function is One-to-One

To ensure a function has an inverse, it must be one-to-one, meaning each element of the domain maps to a unique element in the codomain. Here are two ways to check for this:
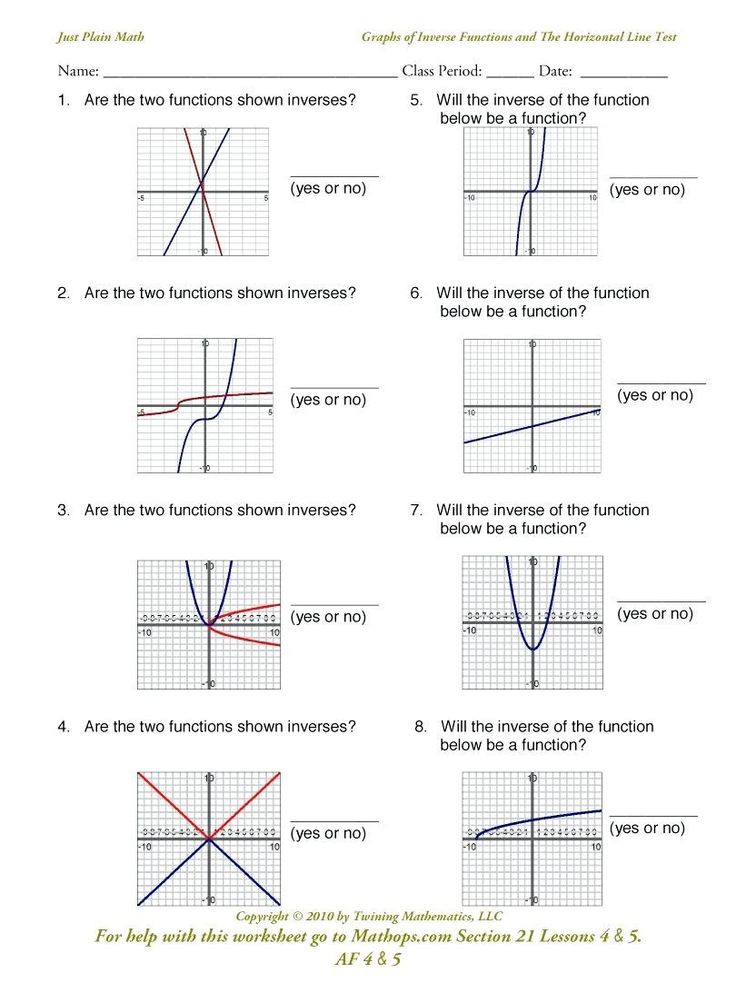
- Use the Horizontal Line Test: If any horizontal line intersects the graph of the function at most once, the function is one-to-one.
- Perform the Calculation Check: For each value x, if f(a) = f(b), then a must equal b.
📝 Note: Not all functions have inverses. If a function fails the one-to-one test, you might need to restrict its domain to make it one-to-one.
2. Replace f(x) with y

Substitute f(x) with y to simplify the function notation during the process of finding the inverse:
y = f(x)
3. Swap x and y
This step effectively reverses the function:
x = f(y)
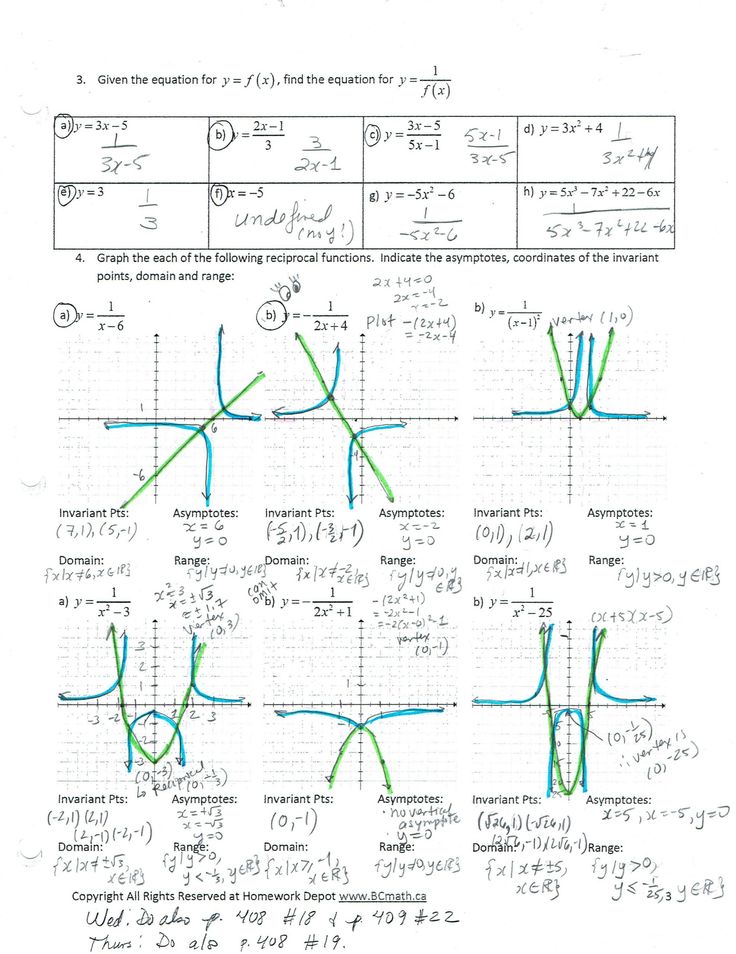
4. Solve for y

Now, solve the equation for y to get the inverse function:
y = f-1(x)
📝 Note: Sometimes, algebraic manipulation can get complicated. Be thorough in your calculations to avoid errors.
Example:

Let's take the function f(x) = 2x + 3:
- Verify One-to-One: This function is linear and, thus, one-to-one.
- Replace f(x) with y: y = 2x + 3
- Swap x and y: x = 2y + 3
- Solve for y:
x - 3 = 2y
(x - 3)/2 = y
y = (x - 3)/2
Thus, f-1(x) = (x - 3)/2
Inverse Functions in Trigonometry

In trigonometry, understanding the inverse functions of sine, cosine, and tangent is crucial:
| Trigonometric Function | Inverse Function | Restricted Domain |
|---|---|---|
| sin(x) | arcsin(x) or sin-1(x) | [-π/2, π/2] |
| cos(x) | arccos(x) or cos-1(x) | [0, π] |
| tan(x) | arctan(x) or tan-1(x) | (-π/2, π/2) |

Graphical Representation of Inverse Functions

The graph of a function and its inverse are symmetric with respect to the line y = x. This means:
- If a point (a, b) lies on f(x), then (b, a) will lie on f-1(x).
- Reflecting the graph of a function f(x) over the line y = x will yield the graph of f-1(x).
Compositions of Inverse Functions

When you compose a function with its inverse, the result should be the identity function:
- f(f-1(x)) = x, for all x in the domain of f-1.
- f-1(f(x)) = x, for all x in the domain of f.
📝 Note: While (f(f-1(x)) = x) is always true, (f-1(f(x)) = x) might not hold true if x is not in the range of f(x).
As we delve deeper into the study of mathematics, we find that the concept of inverse functions is not only fascinating but also extremely useful. The ability to reverse a function allows us to solve for unknown values, understand the behavior of functions better, and apply mathematical models to real-world problems. Whether you're solving complex equations, modeling natural phenomena, or optimizing algorithms, understanding inverse functions provides a toolkit for problem-solving that transcends basic algebra into the realms of calculus, complex analysis, and beyond. By mastering inverse functions, you not only enhance your mathematical prowess but also equip yourself with a universal tool applicable in numerous fields of study and applications.
What is the significance of the Horizontal Line Test in finding inverse functions?

+
The Horizontal Line Test helps determine if a function is one-to-one, which is necessary for having an inverse. If a horizontal line can intersect the graph of a function more than once, it means that at least one output value has multiple input values, thus failing the one-to-one property.
Can a function have more than one inverse?

+
No, a function can have at most one inverse. If a function is one-to-one, it has a unique inverse. If it’s not one-to-one, it doesn’t have an inverse without domain restriction.
How do you find the inverse of non-linear functions like trigonometric ones?

+
The process for non-linear functions, including trigonometric ones, involves the same steps, but the algebraic manipulation might require special methods. For instance, for trigonometric functions, you restrict their domains to ensure one-to-one behavior, and use identities and algebraic manipulation to solve for the inverse.



