5 Key Answers for Similarity Worksheet Intro
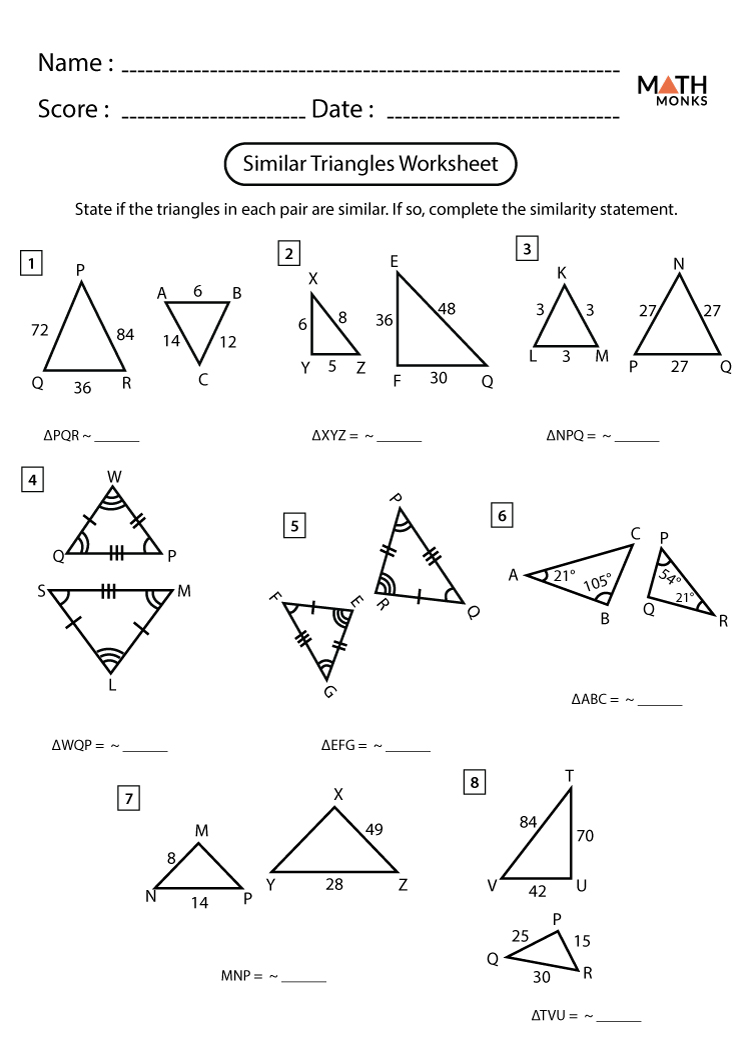
Similarity in mathematics, especially within Geometry, is a powerful concept that involves comparing the proportions and shapes of geometric figures. For students, understanding how to determine if figures are similar can unlock new insights into problem-solving and spatial reasoning. This guide delves into five key answers for a similarity worksheet introduction, providing a foundational understanding necessary for mastering this topic.
The Concept of Similarity


Before we dive into specific answers, let’s outline what it means for two figures to be similar:
- Shape retention: The figures maintain the same shape, though sizes can vary.
- Proportions: Corresponding sides of similar figures are proportional.
- Angles: All corresponding angles are congruent, meaning they have the same measure.
📚 Note: While the size might change, the ratio between corresponding sides remains consistent in similar figures.
Key Answer #1: Similar Triangles

| Triangle ABC | Triangle DEF |
|---|---|
| AB = 3 cm | DE = 6 cm |
| BC = 4 cm | EF = 8 cm |
| CA = 5 cm | FD = 10 cm |
| ∠A = 60° | ∠D = 60° |

From this table, we can see:
- The ratio of corresponding sides (AB/DE, BC/EF, CA/FD) is constant at 1:2.
- Both triangles have an angle measure of 60°, proving angle congruency.
Hence, the triangles ABC and DEF are similar by Side-Side-Side (SSS) similarity criterion.
Key Answer #2: Proportions in Similar Polygons

Similarity extends beyond triangles to any polygon:
- Every pair of corresponding sides of the two polygons must be in proportion.
- The corresponding angles must be equal.
If we have Polygon A with sides 5, 8, 10 cm and Polygon B with sides 15, 24, 30 cm, they are similar as each side’s ratio (5⁄15, 8⁄24, 10⁄30) equals 1:3.
Key Answer #3: Angle-Angle (AA) Similarity Postulate

In triangle similarity, the AA postulate is crucial:
- If two angles of one triangle are congruent to two angles of another, the triangles are similar.
📐 Note: This rule can be applied even if the triangles differ significantly in size, emphasizing angle equality over side length.
Key Answer #4: Proving Similarity in Circles

Circles and arcs can also be similar:
- Two circles are always similar because any line drawn from the center will be proportionate in all circles.
- Arcs of circles are similar if they share the same central angle.
Thus, proving similarity in circles often involves comparing these ratios and angles.
Key Answer #5: Real-Life Applications

Understanding similarity isn’t just for the classroom:
- Architecture uses scaling to model buildings.
- Mapping and geography employ similarity to represent large areas in a reduced format.
- Optics and light refraction involve principles of similarity, where light rays are refracted at similar angles.
These applications highlight how similarity in geometry can inform and influence the real world.
Throughout this exploration, we've uncovered how the principle of similarity governs not just triangles, but all geometric figures, offering practical applications in various fields. Mastery of this concept provides a deeper appreciation for geometric patterns and their implications. From the proportionate sides of similar figures to the uniform angles shared between them, similarity offers a reliable way to connect the abstract world of geometry with the concrete reality we experience daily.
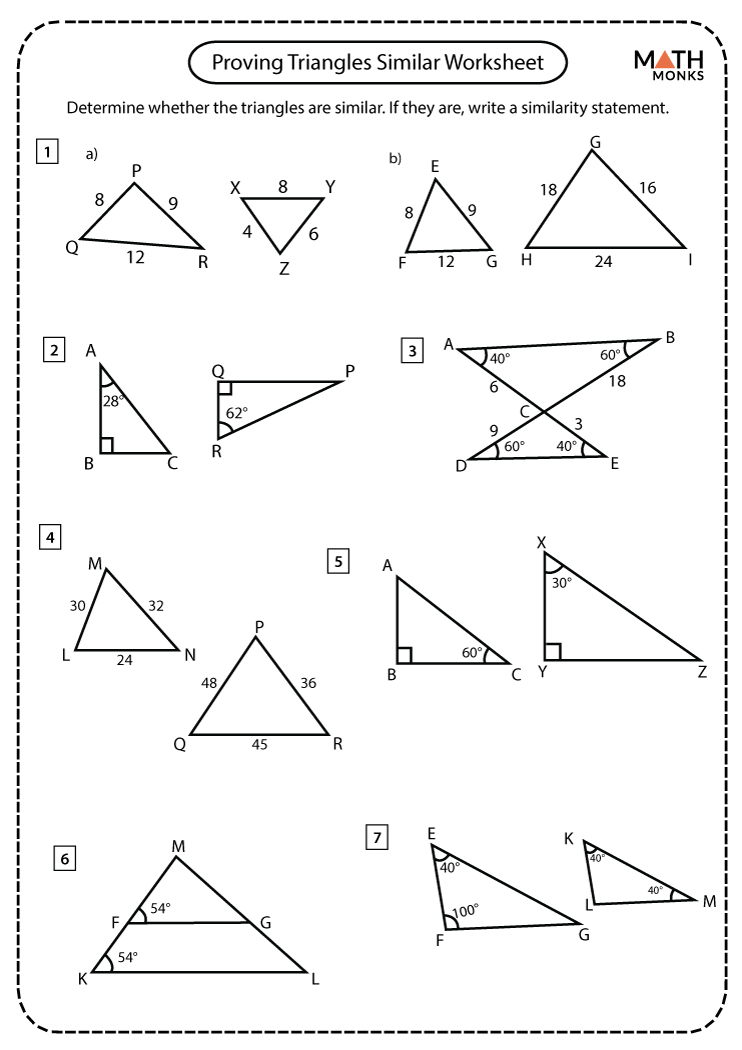
What does it mean for two shapes to be similar?
+
Two shapes are similar if they have the same shape, even if they are different in size. This means their corresponding angles are equal, and their sides are proportional.
Can two polygons be similar if they have different numbers of sides?

+
No, for polygons to be similar, they must have the same number of sides. The proportion of corresponding sides and the equality of corresponding angles apply only to polygons with an identical number of sides.
What is the difference between congruent and similar figures?

+
Congruent figures are both the same shape and size, with identical side lengths and angles. Similar figures, however, only need to have the same shape; their sizes can differ, and their sides must be in proportion.