Mastering Fractions: Beginner's Worksheet Guide

In this comprehensive guide, we will delve into the fascinating world of fractions. Understanding fractions is crucial in mastering math, which provides the foundation for more advanced mathematical concepts. This blog post will equip beginners with the knowledge and practice needed to become proficient with fractions.
What Are Fractions?


Fractions represent parts of a whole. They are used in daily life for measurements, in recipes, and are key elements in various fields like engineering, architecture, and finance. A fraction consists of two parts: the numerator and the denominator:
- Numerator: The top number indicates how many parts of the whole you are considering.
- Denominator: The bottom number shows into how many parts the whole is divided.
🍰 Note: For instance, in the fraction 1⁄4, 1 is the numerator, and 4 is the denominator, representing 1 out of 4 parts of the whole.
Types of Fractions

- Proper Fractions: Where the numerator is less than the denominator, like 2⁄5 or 7⁄9.
- Improper Fractions: The numerator is greater than or equal to the denominator, for example, 5⁄3 or 10⁄10.
- Mixed Numbers: A combination of a whole number and a fraction, such as 2 3⁄4, which means 2 wholes plus 3⁄4 of another whole.
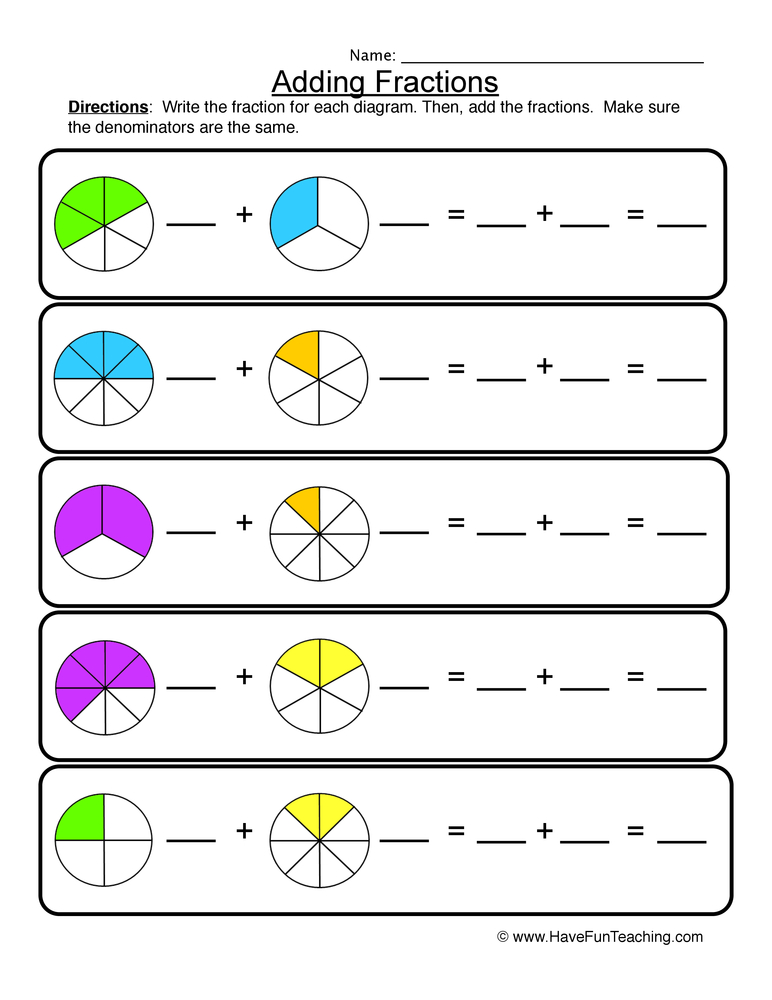
Adding and Subtracting Fractions

Adding or subtracting fractions requires the denominators to be the same (a common denominator). Here’s how:
Steps:

- Find a common denominator.
- Convert each fraction into an equivalent fraction with this common denominator.
- Add or subtract the numerators.
- Keep the denominator the same.
- Simplify the resulting fraction if possible.
📚 Note: Simplifying fractions is essential. A fraction in its simplest form has no common factors other than 1 between the numerator and the denominator.
Multiplying Fractions
Multiplication of fractions is straightforward:
Steps:
- Multiply the numerators of the fractions.
- Multiply the denominators.
- Simplify the resulting fraction.
| Example | Numerator Multiplication | Denominator Multiplication | Result |
|---|---|---|---|
| 1/2 × 3/4 | 1 × 3 = 3 | 2 × 4 = 8 | 3/8 |

Dividing Fractions

Dividing fractions involves inverting the second fraction (called taking the reciprocal) and then multiplying:
Steps:

- Take the reciprocal of the divisor fraction.
- Multiply the numerators.
- Multiply the denominators.
- Simplify the resulting fraction.
🔍 Note: This process can be expressed as: a/b ÷ c/d = a/b × d/c.
Converting Between Mixed Numbers and Improper Fractions

There are times when you’ll need to convert between these forms:
- From Mixed to Improper: Multiply the whole number by the denominator, add this to the numerator, and place the result over the same denominator.
- From Improper to Mixed: Divide the numerator by the denominator. The quotient is the whole number, the remainder becomes the new numerator, and the denominator remains the same.
Practice With Worksheets

Mastering fractions is best achieved through consistent practice:
Recommended Activities:

- Fill in the Blank Worksheets: These provide a basic understanding of fractions.
- Match Up Exercises: Match fractions to their visual representations.
- Word Problems: Practical application of fraction concepts.
- Conversion Challenges: Convert between improper fractions and mixed numbers.
🖍️ Note: Using manipulatives like fraction bars or pies can make practice more engaging and help visualize fractions.
Tips for Success

- Visualize: Use visual aids to understand fractions better.
- Keep Practicing: Regular exercises will reinforce your skills.
- Understand Concepts: Grasp the concepts rather than memorizing formulas.
- Ask Questions: If you’re unsure, ask for clarification.
- Use Real Life Examples: Apply fractions to real-life scenarios to see their practical use.
The journey to mastering fractions involves learning their definitions, understanding how to manipulate them through various operations, and practicing repeatedly. With the right approach and consistent effort, anyone can conquer this mathematical concept. Remember, like any other skill, it takes time and practice to master. Keep your practice varied and enjoyable, and you'll find the world of fractions opening up in no time.
Why are fractions important in daily life?

+
Fractions are essential for various daily activities like cooking (measuring ingredients), budgeting (allocating resources), time management (scheduling), and many other areas where dividing quantities is necessary.
How can I simplify fractions?

+
To simplify fractions, find the greatest common divisor (GCD) of the numerator and denominator, then divide both by this number until they have no common factors other than 1.
What’s the difference between a proper fraction and an improper fraction?

+
A proper fraction has a numerator smaller than the denominator (e.g., 3⁄4), while an improper fraction has a numerator equal to or greater than the denominator (e.g., 7⁄3).



