Intervals of Increase and Decrease: Master Your Calculus Skills

Understanding intervals of increase and decrease is crucial for mastering calculus, as it provides insights into the behavior of functions, their slopes, and how they change over time. This foundational concept helps in analyzing optimization problems, interpreting derivative information, and even predicting trends in real-world scenarios.
What Are Intervals of Increase and Decrease?

When you analyze a function to find intervals of increase and decrease, you’re essentially looking at where the function’s values are either going up or down:
- Intervals of Increase: This is when the function's output increases as the input increases. Mathematically, if f(x) is increasing on an interval I, then for all a and b in I where a < b, f(a) < f(b).
- Intervals of Decrease: This happens when the function's output decreases as the input increases. In terms of calculus, f(x) is decreasing on an interval I if for any a and b where a < b in I, f(a) > f(b).
How to Determine Intervals of Increase and Decrease

To find these intervals, follow these steps:
1. Find the Derivative

Derivatives tell us the rate of change of a function. The first derivative is particularly useful:
- If f'(x) > 0, then f(x) is increasing.
- If f'(x) < 0, then f(x) is decreasing.
2. Solve for Critical Points
Set the first derivative equal to zero and solve for (x) to find where the function might change from increasing to decreasing or vice versa.
3. Test the Intervals

Use the critical points to break the function’s domain into intervals:
- Evaluate the sign of f'(x) within each interval.
- If f'(x) > 0 over the interval, f(x) is increasing.
- If f'(x) < 0 over the interval, f(x) is decreasing.
⚠️ Note: Remember to test the endpoints of the intervals for continuous functions, as they might also be critical points.
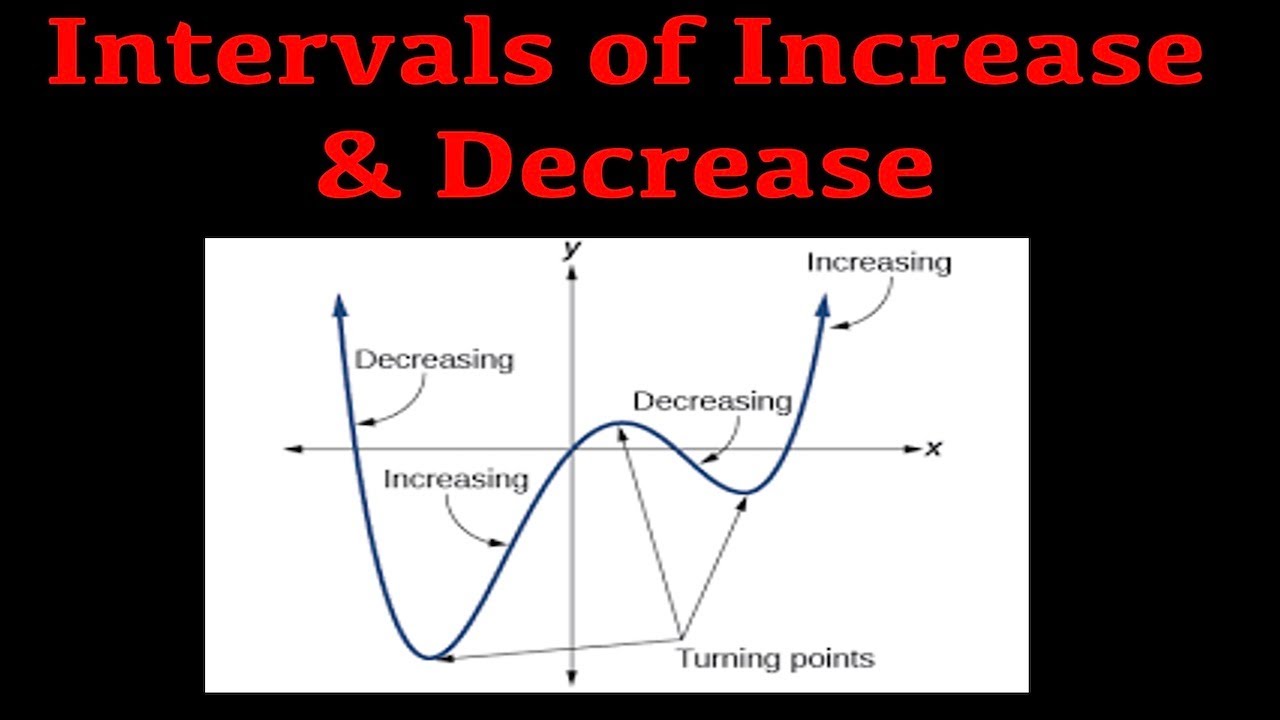
Visualizing with a Graph

A visual representation can clarify these concepts:
- Graphing software or a graphing calculator can plot the function and its derivative. Look for:
- Positive regions for f'(x) indicating increase.
- Negative regions for f'(x) indicating decrease.
Application in Optimization

Understanding increase and decrease is essential in optimization:
Local Maxima and Minima

A function changes from increasing to decreasing or vice versa at these points:
- If f'(x) changes from positive to negative, it's a local maximum.
- If f'(x) changes from negative to positive, it's a local minimum.
Graphing Intervals

Here’s how these concepts are depicted on a graph:
| Interval | Behavior | Description |
|---|---|---|
| (a, b) | Increasing | f'(x) > 0 |
| (c, d) | Decreasing | f'(x) < 0 |
| \{[x_1, x_2]\} | Local Max | Changes from increasing to decreasing |
| \{[x_3, x_4]\} | Local Min | Changes from decreasing to increasing |

Practical Examples

Let’s examine a practical example using a common function:
Example: Quadratic Function

Consider the function (f(x) = x^2 - 4x + 3):
- Calculate the first derivative: f'(x) = 2x - 4.
- Set to zero to find critical points: 2x - 4 = 0 \Rightarrow x = 2.
- Test intervals:
- For x < 2, f'(x) < 0; f(x) decreases.
- For x > 2, f'(x) > 0; f(x) increases.
🔍 Note: Quadratic functions open upward or downward, influencing their intervals of increase and decrease.
Summing Up the Knowledge

The essence of mastering calculus through intervals of increase and decrease lies in understanding how a function behaves over its entire domain. By learning to find where a function is increasing or decreasing, you gain crucial insights into optimization, graph analysis, and real-life applications like economics or physics. This knowledge not only helps in interpreting derivatives but also in solving complex problems where understanding the change rate is key.
How do I know if a function is increasing or decreasing?

+
Analyze the first derivative of the function. If the derivative is positive over an interval, the function is increasing; if it’s negative, the function is decreasing.
What are critical points, and why are they important?

+
Critical points are where the function’s derivative is zero or undefined. They indicate potential changes in the function’s behavior from increasing to decreasing or vice versa, which are essential for optimization problems.
Can a function change its behavior at infinity?

+
Yes, a function can exhibit different behaviors as (x) approaches positive or negative infinity. This often depends on the function’s degree and leading coefficients. Understanding the limit behavior is key in calculus.