5 Essential Tips for Interpreting Histograms Easily

Histograms are powerful visual tools used in statistics to represent the distribution of a dataset. Understanding histograms can provide insights into data patterns, spread, and potential outliers. Here are five essential tips to interpret histograms easily and effectively.
Understand the Structure

Before diving into analysis, it’s crucial to comprehend the basic structure of a histogram:
- Bins: Histograms divide data into continuous intervals or bins. Each bin represents a range of data values.
- Frequency: The height of each bin indicates the number of data points within that interval.
- Vertical Axis: Shows the frequency or relative frequency.
- Horizontal Axis: Represents the range of data divided into bins.
Examine the Shape

Analyzing the shape of a histogram can reveal a lot about the data:
- Symmetry: A symmetrical histogram suggests a balanced distribution.
- Skewness: Skewness to the left indicates a longer tail towards lower values (positively skewed), while skewness to the right indicates higher values (negatively skewed).
- Normality: A bell-shaped histogram might imply data normality, although not all bell shapes guarantee normality.
- Peaks and Troughs: Multiple peaks (bimodal or multimodal distributions) can indicate different groups or subpopulations within the data.
⚠️ Note: Remember, skewness can be misleading if not interpreted correctly; always consider the context of the data.
Look for Outliers and Gaps
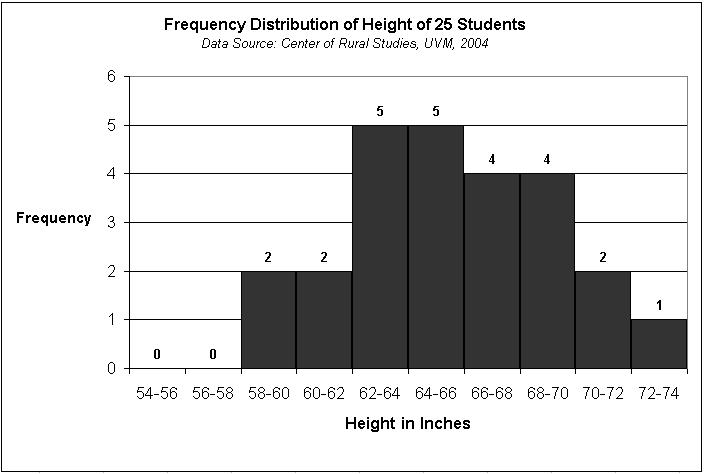
Outliers and gaps in data can significantly affect your interpretation:
- Outliers: Data points far from the bulk of the data might appear as single bars detached from the main cluster.
- Gaps: Intervals with zero frequency can indicate missing values or a real absence of data in that range.
- Clusters: Multiple clusters might suggest the presence of different groups within the dataset.
| Histogram Feature | Interpretation |
|---|---|
| Isolated Bars | Likely outliers or data entry errors |
| Gaps | Potential for missing data or natural breaks in data distribution |

Compare with Known Distributions

Histograms can help compare your data distribution with known theoretical distributions:
- Normal Distribution: Overlaid with a normal curve to see how well the data fits.
- Uniform Distribution: Data spread uniformly across bins.
- Exponential or Power-Law Distributions: Characteristics of phenomena with rapid decay or heavy-tailed data.
💡 Note: Overlaying a theoretical curve on your histogram can visually help identify the distribution type.
Utilize Visual Enhancements
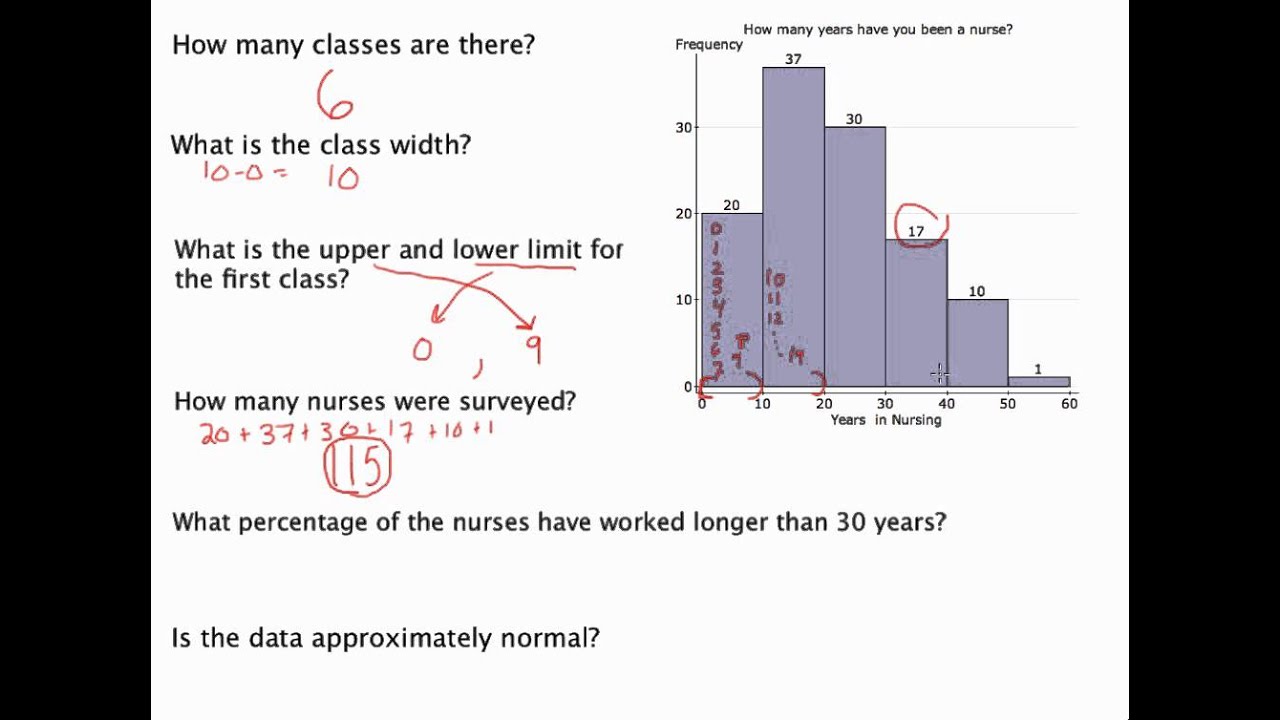
To aid interpretation:
- Color Coding: Use different colors for different aspects of the data, like different categories or sources.
- Annotations: Add notes or lines to highlight key features like mean, median, mode, or thresholds.
- Zoom and Pan: Modern tools allow interaction with histograms to zoom in or pan, making subtle features more visible.
In summary, interpreting histograms involves understanding their structural components, examining the data distribution for skewness or symmetry, identifying outliers and gaps, comparing with known statistical distributions, and using visual tools to enhance readability. These tips are designed to help anyone from beginners to seasoned analysts to interpret histograms with ease, allowing for more accurate data analysis and decision-making.
How do I know if my data is normally distributed from a histogram?

+
Look for a bell-shaped curve. If your histogram closely resembles a symmetric bell shape, especially with a smooth single peak, this could indicate that your data is normally distributed. However, histograms provide only visual cues; statistical tests like the Shapiro-Wilk test or Q-Q plots are needed for confirmation.
What do gaps in a histogram suggest?

+
Gaps in a histogram could suggest missing data, data entry errors, or naturally occurring breaks in the data distribution. It can also indicate the presence of categorical data or different subpopulations in your sample.
Can histograms tell me about the mean, median, or mode?

+
While histograms don’t explicitly show mean, median, or mode, you can estimate: - Mean: Often around the midpoint of the symmetric part. - Median: Can be roughly estimated where the histogram divides into two equal areas. - Mode: The tallest bin or peak in the histogram.



