Unlock Polygon Secrets: Angles Worksheet Mastery
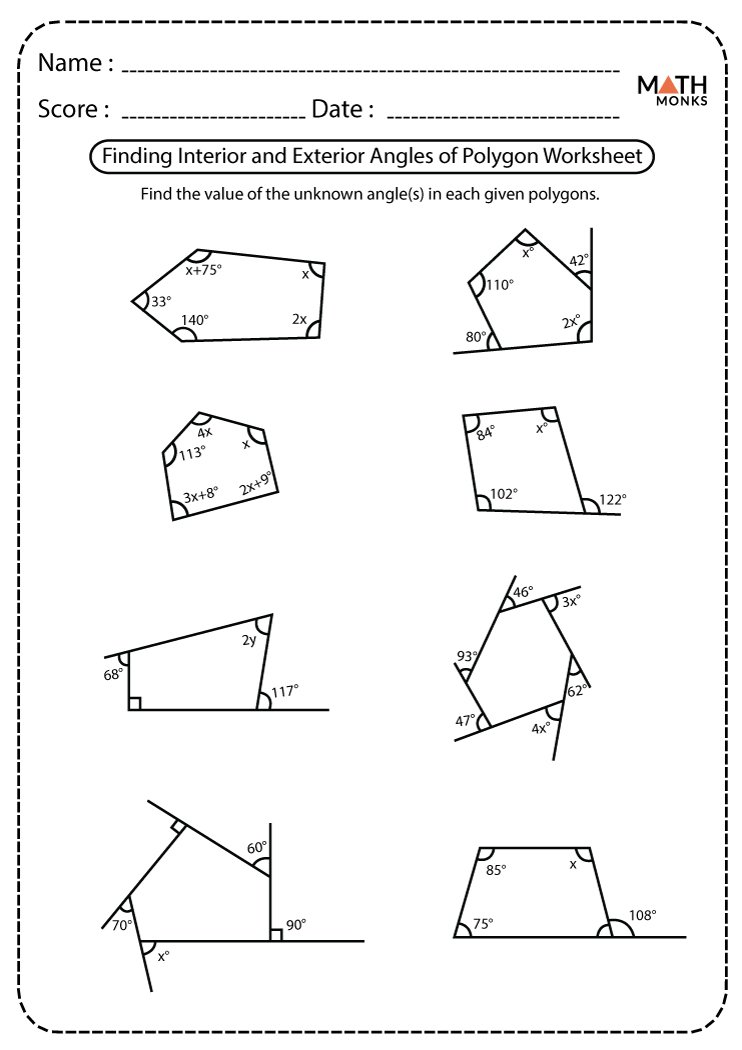
Mastering angles in polygons is a fundamental skill for students learning geometry. Whether you're preparing for a class, a competitive exam, or just brushing up on your geometry knowledge, understanding how to work with angles in polygons is crucial. This detailed guide will walk you through everything from basic definitions to solving complex problems involving polygon angles. Let's unlock these secrets together!
Why Angles in Polygons Matter
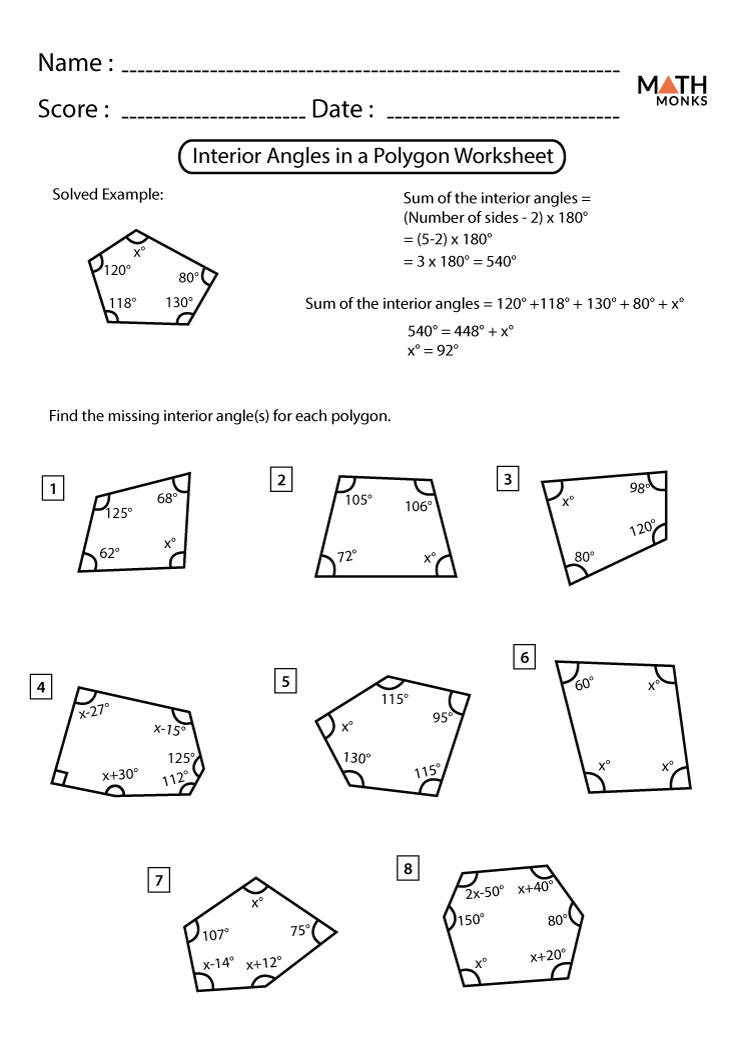
Angles within polygons are not just a theoretical construct; they are integral to understanding space, design, architecture, and numerous practical applications. Here’s why mastering angles in polygons is essential:
- Practical Applications: From architects designing buildings to graphic designers creating symmetrical logos, understanding angles helps in creating functional and visually pleasing structures.
- Mathematical Foundation: Knowledge of polygon angles is a stepping stone to higher mathematics, including trigonometry, analytical geometry, and even calculus.
- Problem Solving: Working with polygons hones logical thinking and problem-solving skills, which are vital in various fields outside of mathematics.

Understanding Polygon Basics

A polygon is a plane figure that is bounded by a closed path or circuit, composed of a finite sequence of straight line segments. Here are some key aspects to understand:
- Vertices: The points where two sides meet.
- Edges (Sides): The line segments connecting two vertices.
- Interior Angles: The angles formed inside the polygon at each vertex.
- Exterior Angles: The angles formed outside each vertex of the polygon.
The Sum of Interior Angles

The sum of the interior angles of a polygon can be found using the formula:
Sum of Interior Angles = 180° (n - 2)
Where n is the number of sides in the polygon. Here’s how you can understand and apply this:
- For a triangle (n=3): 180° (3 - 2) = 180°
- For a pentagon (n=5): 180° (5 - 2) = 540°
📚 Note: Remember, this formula gives you the total sum of all interior angles in degrees.
Exterior Angles and Their Properties

Each exterior angle of a polygon adds up to 360°, regardless of the polygon’s shape or the number of sides:
- For any polygon: Sum of Exterior Angles = 360°
The measure of each exterior angle can be calculated by:
Exterior Angle = 360° / n
Angles Worksheet Mastery: Step-by-Step Guide

Here’s a practical guide to mastering angle problems in polygons:
- Identify the Polygon: Count the number of sides and label each vertex clearly.
- Use Formulas: Apply the formula for interior or exterior angles based on what is required in the problem.
- Solve for Unknowns: If some angles are given, calculate the unknown angles using the sum properties.
- Check Your Work: Ensure that the total sum of angles or the relationship between interior and exterior angles holds true.
🔍 Note: Always double-check your calculations by summing all angles or verifying exterior angle properties.
| Polygon | Sum of Interior Angles | Each Exterior Angle |
|---|---|---|
| Triangle | 180° | 120° |
| Quadrilateral | 360° | 90° |
| Pentagon | 540° | 72° |

Applying Polygon Angle Knowledge

Let’s apply what we’ve learned in a few practical examples:
- Regular Pentagon: If all sides and angles are equal, find each interior angle.
- Irregular Heptagon: Given several angles, solve for the unknown angles.
- Central Angle in a Circle: Use polygon properties in problems involving sectors and arcs.
💡 Note: In a regular polygon, all sides and angles are equal, making calculations easier.
In Summary

Mastering angles in polygons isn’t just about recalling formulas; it’s about understanding the geometry of shapes and how these properties apply in real-world scenarios. From ensuring structural stability in architecture to creating aesthetically pleasing designs, the angles in polygons play a crucial role. By breaking down the concepts, applying formulas systematically, and practicing various types of problems, students and professionals alike can unlock the full potential of polygon geometry, enhancing their spatial and analytical skills.
What is the difference between interior and exterior angles?

+
Interior angles are the angles formed inside the polygon at each vertex, while exterior angles are those formed by extending one side of the polygon and measuring the angle between the extended side and the adjacent side.
How can I use the sum of angles to check if a shape is a polygon?

+
If the sum of interior angles for a shape matches the formula (180° (n - 2)) where n is the number of sides, then the shape is a polygon. Also, the sum of exterior angles should always be 360°.
Why is knowing the exterior angles useful?

+
Exterior angles are particularly useful in problems involving rotation or when finding the measure of individual angles in regular polygons. They also help in understanding the geometry of tessellations and patterns.