Mastering Integer Exponents: Fun Worksheet Challenges

In the realm of mathematics, integer exponents are a fundamental concept, essential for understanding algebraic expressions, simplifying problems, and even tackling complex mathematical models. Mastering integer exponents not only helps in academic pursuits but also sharpens logical thinking and problem-solving skills. Today, we dive into some fun worksheet challenges designed to boost your understanding and proficiency with integer exponents.
Understanding Integer Exponents
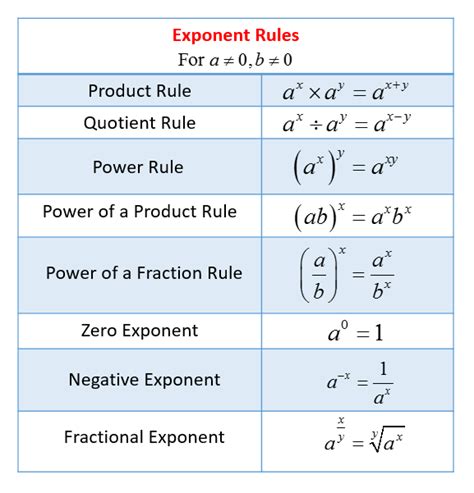
Before we leap into the worksheets, let's quickly recap what integer exponents are:
- Base: The number being raised to a power.
- Exponent: The power to which the base is raised.
- Positive Exponents: Indicate multiplication, e.g., 2^3 = 8.
- Negative Exponents: Represent the reciprocal, e.g., 2^{-3} = \frac{1}{8}.
Worksheet Challenges

Challenge 1: Positive and Negative Exponents

Let's start with a basic exercise to strengthen your base understanding:
| Expression | Answer |
|---|---|
| 42 | 16 |
| 3-2 | 1/9 |
| (-2)3 | -8 |
| (-5)-1 | -1/5 |

Try these problems on your own:
- 82
- 7-3
- (-4)2
- (-1)-4
💡 Note: Remember, a negative exponent does not change the sign of the base if the base is negative.
Challenge 2: Combining Exponents

Now, let's tackle some problems that require you to combine exponents:
| Expression | Answer |
|---|---|
| 32 * 33 | 35 = 243 |
| (23)2 | 26 = 64 |
| 52 / 54 | 5-2 = 1/25 |
Try these problems on your own:
- 24 * 22
- (52)3
- 65 / 62
Challenge 3: Application in Real-Life Problems

Here's where things get exciting. Let's apply integer exponents to real-life scenarios:
Problem 1: If you have a smartphone battery that loses 2% of its charge every hour, how much charge remains after 5 hours?
- 100% * (1 - 0.02)5 = 100% * 0.985 ≈ 90.4%
Problem 2: The half-life of a radioactive substance is 8 minutes. How much of the substance remains after 24 minutes?
- Initial amount * 0.53 = Initial amount * 1/8
🔬 Note: In scientific applications, integer exponents often represent quantities that are multiplied or divided by a constant factor, making it a powerful tool for modeling growth or decay.
Challenge 4: Fractional Exponents

Understanding fractional exponents provides insight into roots:
- 21/3 = cube root of 2 ≈ 1.26
- 91/2 = square root of 9 = 3
- (8)2/3 = (81/3)2 = 22 = 4
Try these problems on your own:
- 161/2
- 271/3
- 813/4
In this exploration of integer exponents, we've covered the basic rules and ventured into more complex applications, demonstrating the power and utility of this mathematical concept. Mastery over integer exponents unlocks doors to understanding not just algebraic equations but also the dynamics of real-world phenomena. Whether it's calculating financial growth, physical decay, or geometric sequences, integer exponents are your silent ally.
What is the difference between positive and negative exponents?

+
Positive exponents indicate repeated multiplication of the base by itself, while negative exponents indicate the reciprocal of the same repeated multiplication. For example, 43 = 4 * 4 * 4 = 64, and 4-3 = 1/(4 * 4 * 4) = 1⁄64.
How do I combine exponents when multiplying?

+
When multiplying two expressions with the same base, you add the exponents. For instance, 32 * 33 = 3(2+3) = 35.
What are fractional exponents used for?

+
Fractional exponents represent roots of a number. For example, 81⁄3 is the cube root of 8, which is 2. If the exponent is a fraction like 3⁄4, you can interpret it as taking the fourth root of the number and then cubing the result.