Easily Convert Improper Fractions to Mixed Numbers with This Worksheet

Understanding how to convert improper fractions to mixed numbers is a fundamental math skill that's useful in various mathematical operations, from basic arithmetic to advanced algebra. This skill not only aids in solving mathematical problems but also in real-world applications such as cooking, crafting, or measuring. This blog post will guide you through an interactive and fun worksheet method to convert improper fractions into mixed numbers, ensuring you grasp the concept thoroughly.
Why Convert Improper Fractions to Mixed Numbers?

Before diving into the conversion, let's understand why it's beneficial:
- Clarity: Mixed numbers provide a clearer picture than improper fractions, especially when dealing with quantities more than one.
- Practical Use: In everyday scenarios, such as splitting a pizza among friends, mixed numbers are more intuitive.
- Problem Solving: Many mathematical problems require answers in mixed numbers for better understanding and application.
Steps to Convert Improper Fractions to Mixed Numbers

Here is a simple, five-step process to convert improper fractions into mixed numbers:
Step 1: Identify the Numerator and Denominator

The first step in converting an improper fraction to a mixed number is to identify the numerator (the top number) and the denominator (the bottom number). For example, let’s consider the fraction 11⁄3.
Step 2: Perform the Division
Divide the numerator by the denominator. In our example:
- 11 ÷ 3 gives us a quotient of 3, with a remainder of 2.
Step 3: Write Down the Whole Number

The quotient from the division is the whole number part of your mixed number. Here, it’s 3.
Step 4: Use the Remainder as the New Numerator

The remainder becomes the numerator of the fraction part of your mixed number. So, the fraction part is 2⁄3.
Step 5: Combine to Form the Mixed Number

Combine the whole number and the fraction to form the mixed number: 3 2⁄3.
🔗 Note: This process can be applied to any improper fraction. The larger the numerator, the bigger the whole number part of your mixed number will be.
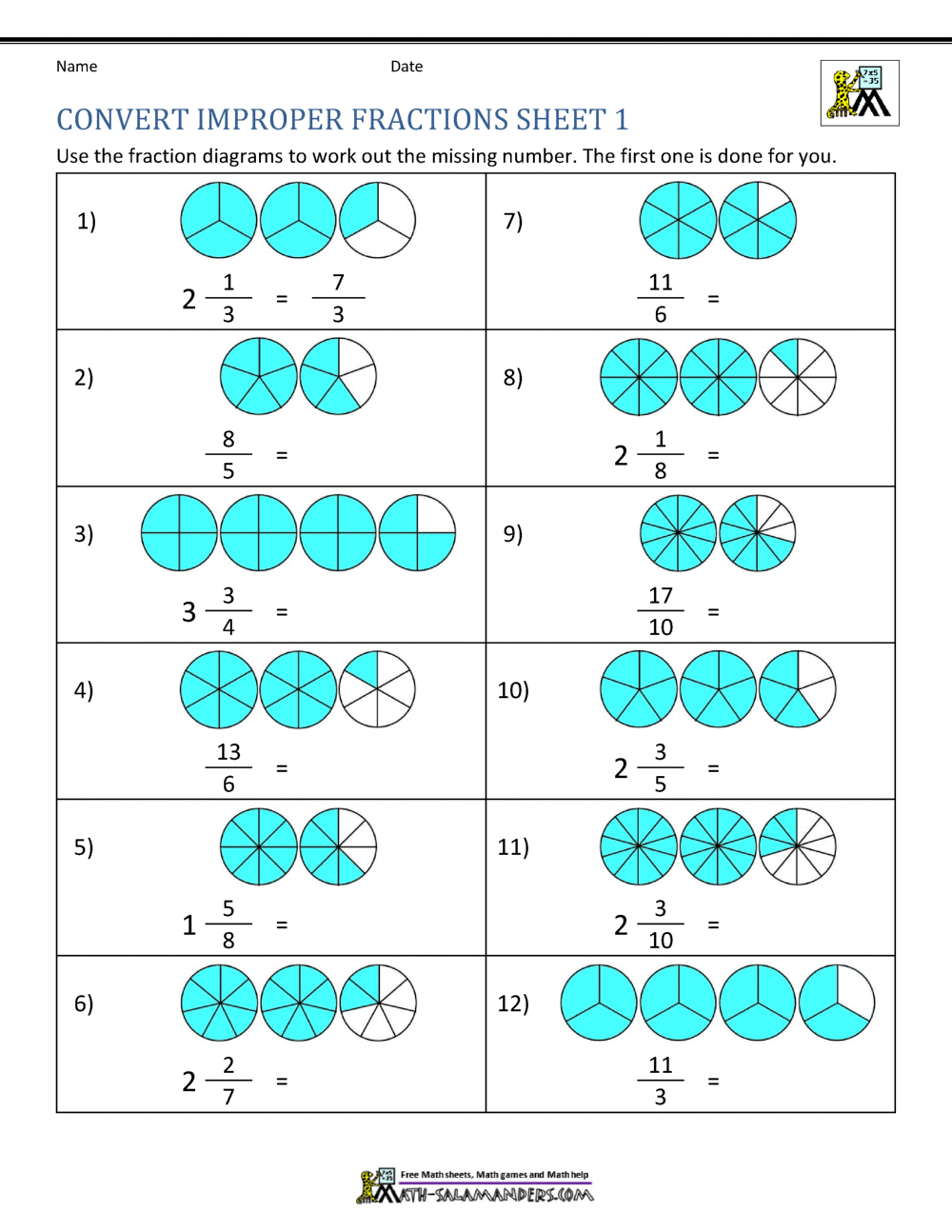
Worksheet for Practicing Conversion

| Improper Fraction | Whole Number | Remainder | Mixed Number |
|---|---|---|---|
| 11/3 | 3 | 2 | 3 2/3 |
| 7/2 | |||
| 17/5 | |||
| 9/4 | |||
| 25/6 |

To fill out the above table:
- Divide the numerator by the denominator for each improper fraction.
- Record the quotient as the whole number.
- Write down the remainder.
- Form the mixed number using the steps provided.
🔍 Note: For practice, you can invent your own improper fractions or use these examples to verify your understanding of the conversion process.
Tips for Teaching and Learning

Here are some useful tips when teaching or learning this conversion:
- Visual Aids: Use pie charts, blocks, or any visual representation to show division.
- Engage with Real-World Examples: Use real-world scenarios to illustrate the need for mixed numbers.
- Online Tools: Consider using online tools or apps designed for fraction conversion to enhance learning through interactivity.
Mastering the conversion of improper fractions to mixed numbers not only enriches your mathematical toolkit but also equips you to handle practical situations with greater ease. Whether it's splitting items evenly or solving complex math problems, understanding mixed numbers will certainly come in handy.
Why are mixed numbers sometimes preferred over improper fractions?

+
Mixed numbers represent a whole number plus a proper fraction, making it easier to visualize quantities more than one. This format is often more intuitive in everyday contexts like sharing or measuring.
Can all improper fractions be converted to mixed numbers?

+
Yes, any fraction where the numerator is greater than or equal to the denominator can be converted into a mixed number. The method involves division, making the conversion straightforward.
How do you convert mixed numbers back to improper fractions?

+
To convert a mixed number back to an improper fraction, multiply the whole number by the denominator of the fraction, add the result to the numerator, and then place that number over the original denominator. For example, 3 2⁄3 becomes (3 x 3 + 2)/3 = 11⁄3.