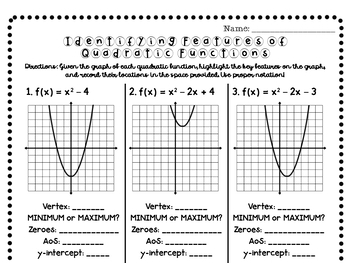
5 Key Features of Quadratic Functions Unveiled

Quadratic functions, with their unique shape and behavior, are integral in various fields such as physics, engineering, economics, and daily life scenarios like the path of a thrown ball or the parabolic shape of a bridge. Understanding the features of quadratic functions can significantly enhance problem-solving capabilities, analytical skills, and model conceptual understanding. Here, we explore five key features of quadratic functions, offering a comprehensive look into their fundamental aspects.
1. The Standard Form

A quadratic function can be represented in various forms, but the standard form is often the starting point for analysis:
f(x) = ax2 + bx + c
- a: Determines the parabola's direction and width; if a > 0, the parabola opens upward, and if a < 0, it opens downward.
- b: Influences the horizontal position of the vertex and the symmetry axis.
- c: Represents the y-intercept, the point where the parabola intersects the y-axis.
📝 Note: The form ax2 + bx + c is not just a formula but a gateway to understanding the behavior and characteristics of quadratic functions.
2. The Vertex

The vertex is arguably the most critical feature of a quadratic function. It represents either the maximum or minimum point of the parabola, which is essential for various applications:
- The vertex formula can be derived from the standard form:
- xv = -b/(2a)
- yv = f(xv) = axv2 + bxv + c
Here's a table summarizing the vertex characteristics:
| Direction of Parabola | Vertex Type |
|---|---|
| Upward (a > 0) | Minimum |
| Downward (a < 0) | Maximum |
3. Axis of Symmetry
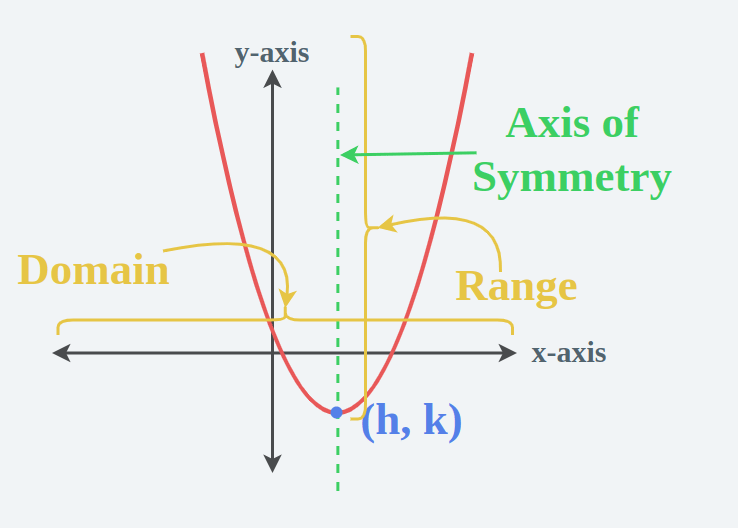
The axis of symmetry, a vertical line passing through the vertex, splits the parabola into two mirror-image halves. Its equation is straightforward:
x = -b/(2a)
- This line acts as a guide for analyzing symmetry in the graph of the quadratic function.
4. The Roots or X-Intercepts

Finding where a quadratic function intersects the x-axis (or the roots) involves solving for x when f(x) = 0. This can be done using several methods:
- The Quadratic Formula: x = [-b ± √(b2 - 4ac)] / (2a)
- Factoring: Identifying two binomials whose product equals the quadratic.
- Completing the Square: Transforming the standard form to an equivalent perfect square trinomial.
📝 Note: Roots can help predict where a function has a zero or positive-negative change, which is crucial in engineering, finance, and many other fields.
5. The Vertex Form

Another representation of a quadratic function is its vertex form, which makes analyzing the vertex more straightforward:
f(x) = a(x - h)2 + k
- (h, k): The coordinates of the vertex.
- a: As in standard form, it indicates the parabola's direction and spread.
Summing up, exploring these five key features of quadratic functions unveils the beauty and utility of these mathematical entities. From understanding the standard form to mastering the vertex form, each characteristic provides invaluable insights into the parabola’s behavior, making it a foundational topic in algebra and beyond. Whether you’re tackling optimization problems or analyzing physical phenomena, these features empower you to describe, predict, and visualize outcomes effectively.
What is the significance of the vertex form of a quadratic function?

+
The vertex form f(x) = a(x - h)2 + k directly provides the vertex’s coordinates, making it easier to analyze the maximum or minimum points of the parabola without using calculus or completing the square.
How do the coefficients affect the parabola’s shape and direction?

+
The coefficient ‘a’ determines the parabola’s width (the smaller the absolute value, the wider the parabola) and direction (positive opens upward, negative opens downward). ‘b’ affects the x-coordinate of the vertex and the axis of symmetry, while ‘c’ is the y-intercept.
Can a quadratic function have more than two roots?

+
No, a standard quadratic function f(x) = ax2 + bx + c can have at most two real roots, corresponding to the points where the parabola intersects the x-axis. However, complex roots can exist when the discriminant (b2 - 4ac) is negative.
Why is understanding quadratic functions important in real life?

+
Quadratic functions model many real-life phenomena, such as projectile motion, optimization problems in economics, parabolic reflectors in satellite dishes, and the strength of arches in architecture. They provide insights into predicting outcomes and solving problems with constraints.