Excel
5 Ways To Subtract
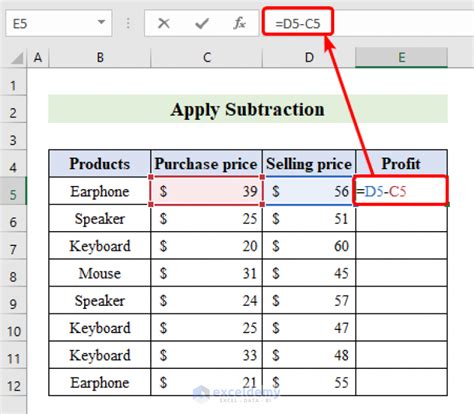
Introduction to Subtraction

Subtraction is a fundamental arithmetic operation that involves finding the difference between two numbers. It is a crucial concept in mathematics and is used extensively in various aspects of life, including science, engineering, economics, and everyday problem-solving. In this article, we will explore five different ways to subtract numbers, highlighting the methods, examples, and applications of each approach.
Method 1: Standard Subtraction

The standard subtraction method is the most common technique used to subtract numbers. It involves subtracting the subtrahend (the number being subtracted) from the minuend (the number from which another is being subtracted). This method can be applied to both positive and negative numbers. For example, to subtract 5 from 10, we perform the calculation: 10 - 5 = 5. This method is straightforward and is widely used in various mathematical operations.
Method 2: Counting Back

The counting back method is a simple and intuitive approach to subtraction. It involves counting back the subtrahend from the minuend. For instance, to subtract 3 from 8, we start with 8 and count back 3 numbers: 8, 7, 6, 5. The result is 5. This method is particularly useful for subtracting small numbers and can be an effective way to introduce subtraction to young learners.
Method 3: Using Number Lines

The number line method is a visual approach to subtraction. It involves representing numbers on a number line and moving to the left to subtract. For example, to subtract 4 from 9, we start at 9 on the number line and move 4 units to the left, landing on 5. This method provides a clear visual representation of the subtraction process and can be helpful for understanding the concept of negative numbers.
Method 4: Decomposing Numbers

The decomposing numbers method involves breaking down numbers into their place values and then subtracting. For instance, to subtract 247 from 543, we can break down the numbers into hundreds, tens, and ones: 500 + 40 + 3 (minuend) and 200 + 40 + 7 (subtrahend). We then subtract the corresponding place values: 500 - 200 = 300, 40 - 40 = 0, and 3 - 7 = -4. Combining the results, we get 300 + 0 - 4 = 296. This method is useful for subtracting larger numbers and can help develop a deeper understanding of place value.
Method 5: Using Mental Math

The mental math method involves using mental calculations to subtract numbers. It involves using various strategies, such as rounding numbers, using benchmarks, or applying subtraction facts. For example, to subtract 19 from 25, we can use the fact that 20 - 19 = 1 and then adjust for the remaining 5: 25 - 19 = 20 - 19 + 5 = 1 + 5 = 6. This method is useful for developing mental calculation skills and can be an efficient way to perform subtraction calculations.
📝 Note: Mental math strategies can vary depending on the individual and the specific calculation, so it's essential to practice and develop your own approaches.
Applications of Subtraction

Subtraction has numerous applications in various fields, including: * Science: Subtraction is used to calculate changes in quantities, such as temperature, distance, or velocity. * Economics: Subtraction is used to calculate profits, losses, and changes in financial values. * Engineering: Subtraction is used to calculate stresses, strains, and changes in physical quantities. * Everyday life: Subtraction is used to calculate expenses, savings, and changes in personal finances.
| Method | Description | Example |
|---|---|---|
| Standard Subtraction | Subtracting the subtrahend from the minuend | 10 - 5 = 5 |
| Counting Back | Counting back the subtrahend from the minuend | 8 - 3 = 5 |
| Number Line | Moving to the left to subtract | 9 - 4 = 5 |
| Decomposing Numbers | Breaking down numbers into place values | 543 - 247 = 296 |
| Mental Math | Using mental calculations to subtract | 25 - 19 = 6 |
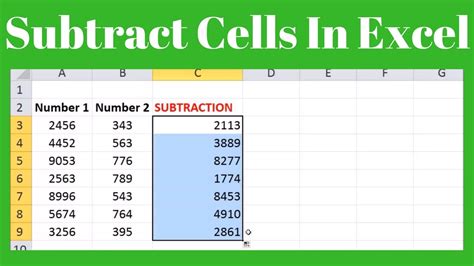
In summary, subtraction is a fundamental arithmetic operation that can be performed using various methods, including standard subtraction, counting back, number lines, decomposing numbers, and mental math. Each method has its own strengths and applications, and understanding these approaches can help develop a deeper understanding of mathematics and improve problem-solving skills. By mastering these methods, individuals can become more proficient in performing subtraction calculations and develop a stronger foundation in mathematics.