5 Ways To Measure Correlation

Introduction to Correlation Measurement

Measuring correlation is a crucial aspect of data analysis, as it helps in understanding the relationship between two variables. Correlation can be either positive, negative, or neutral, and it is essential to use the right methods to measure it accurately. In this blog post, we will discuss five ways to measure correlation, including their applications, advantages, and limitations.

1. Pearson’s Correlation Coefficient

Pearson’s correlation coefficient is the most commonly used method to measure correlation between two continuous variables. It is calculated using the formula: [ r = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{\sqrt{\sum{(x_i - \bar{x})^2}\sum{(y_i - \bar{y})^2}}} ] where (x_i) and (y_i) are individual data points, (\bar{x}) and (\bar{y}) are the means of the two variables. The value of (r) ranges from -1 to 1, where 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no correlation.

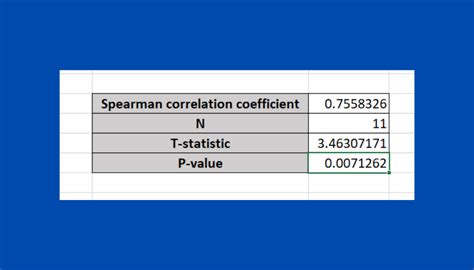
2. Spearman’s Rank Correlation Coefficient

Spearman’s rank correlation coefficient is used to measure correlation between two variables when the data is not normally distributed or when the data is in the form of ranks. It is calculated using the formula: [ \rho = 1 - \frac{6\sum{d_i^2}}{n(n^2 - 1)} ] where (d_i) is the difference between the ranks of the two variables, and (n) is the number of data points. The value of (\rho) also ranges from -1 to 1.

3. Kendall’s Tau Correlation Coefficient

Kendall’s tau correlation coefficient is another non-parametric method used to measure correlation between two variables. It is calculated using the formula: [ \tau = \frac{2P - Q}{\sqrt{P + Q + T}\sqrt{P + Q + U}} ] where (P) is the number of concordant pairs, (Q) is the number of discordant pairs, (T) is the number of ties in the first variable, and (U) is the number of ties in the second variable.

4. Mutual Information

Mutual information is a measure of correlation between two variables based on information theory. It is calculated using the formula: [ I(X;Y) = \sum{p(x,y) \log{\frac{p(x,y)}{p(x)p(y)}}} ] where (p(x,y)) is the joint probability distribution of the two variables, and (p(x)) and (p(y)) are the marginal probability distributions.

5. Distance Correlation

Distance correlation is a measure of correlation between two variables based on the distance between the data points. It is calculated using the formula: [ dCor(X,Y) = \frac{\sqrt{\sum{(x_i - \bar{x})^2(y_i - \bar{y})^2}}}{\sqrt{\sum{(x_i - \bar{x})^2}\sum{(y_i - \bar{y})^2}}} ] The value of (dCor) ranges from 0 to 1, where 0 indicates no correlation and 1 indicates perfect correlation.

📝 Note: The choice of method depends on the nature of the data and the research question. It is essential to understand the assumptions and limitations of each method before applying it to the data.

The following table summarizes the five methods:

Method	Formula	Range
Pearson’s Correlation Coefficient	( r = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{\sqrt{\sum{(x_i - \bar{x})^2}\sum{(y_i - \bar{y})^2}}} )	-1 to 1
Spearman’s Rank Correlation Coefficient	( \rho = 1 - \frac{6\sum{d_i^2}}{n(n^2 - 1)} )	-1 to 1
Kendall’s Tau Correlation Coefficient	( \tau = \frac{2P - Q}{\sqrt{P + Q + T}\sqrt{P + Q + U}} )	-1 to 1
Mutual Information	( I(X;Y) = \sum{p(x,y) \log{\frac{p(x,y)}{p(x)p(y)}}} )	0 to infinity
Distance Correlation	( dCor(X,Y) = \frac{\sqrt{\sum{(x_i - \bar{x})^2(y_i - \bar{y})^2}}}{\sqrt{\sum{(x_i - \bar{x})^2}\sum{(y_i - \bar{y})^2}}} )	0 to 1

In conclusion, measuring correlation is a critical aspect of data analysis, and there are various methods to do so. Each method has its strengths and limitations, and the choice of method depends on the research question and the nature of the data. By understanding the different methods and their applications, researchers can make informed decisions and draw meaningful conclusions from their data.