5 Ways To Curve

Introduction to Curves

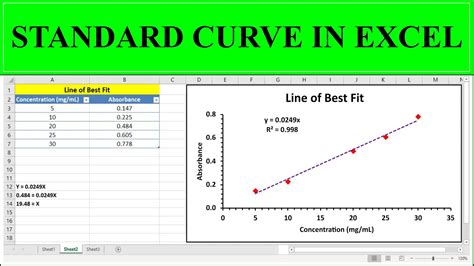
When it comes to design, architecture, and even data analysis, curves play a significant role in creating visually appealing and informative representations. A curve is a continuous, smooth shape that can be used to model real-world phenomena, design innovative products, or simply add an aesthetic touch to a presentation. In this article, we will explore five ways to curve, highlighting their applications, benefits, and how they can be utilized in various fields.

Understanding the Basics of Curves

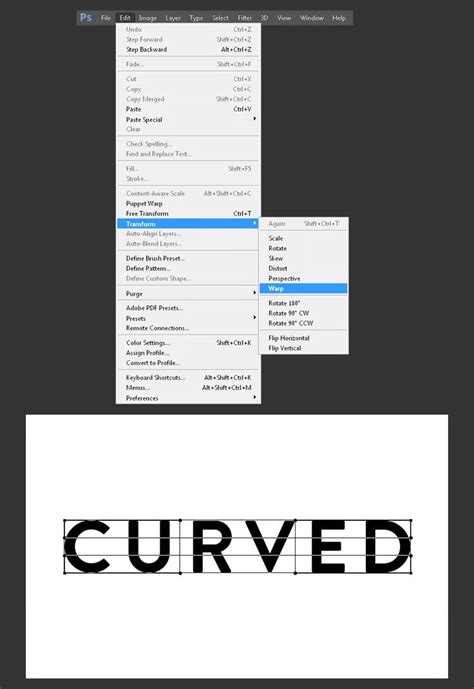
Before diving into the different ways to curve, it’s essential to understand the basics. A curve can be defined as a set of points that are connected by a continuous, smooth line. Curves can be open or closed, planar or non-planar, and can have various degrees of curvature. The degree of curvature refers to how sharply a curve turns, with higher degrees indicating tighter turns.

1. Bezier Curves

Bezier curves are a type of curve used extensively in computer graphics, design, and engineering. They are defined by a set of control points that determine the shape of the curve. Bezier curves are parametric, meaning they are defined by a mathematical equation that takes into account the control points and the parameter (usually time or distance). This allows for smooth and precise control over the curve’s shape, making Bezier curves ideal for designing complex shapes and models.

2. Spline Curves

Spline curves are another type of curve used in various applications, including computer-aided design (CAD), engineering, and data analysis. A spline curve is a piecewise function that connects multiple curves to create a smooth, continuous shape. Spline curves are flexible and adaptable, allowing them to be used in a wide range of applications, from designing car bodies to modeling complex data sets.

3. Elliptical Curves

Elliptical curves are a type of curve that is defined by an ellipse. An ellipse is a closed curve with two focal points, and elliptical curves are used extensively in mathematics, physics, and engineering. Elliptical curves have unique properties, such as being symmetric about their center and having a constant sum of distances from the two focal points. This makes them ideal for modeling real-world phenomena, such as the orbits of planets or the shape of a mirror.

4. Spiral Curves

Spiral curves are a type of curve that winds around a central point, either clockwise or counterclockwise. Spiral curves are found in nature, from the shape of seashells to the structure of galaxies. They are also used in design and architecture, adding a touch of elegance and sophistication to buildings, products, and logos. Spiral curves can be mathematically modeled, allowing designers and engineers to create precise and intricate designs.

5. Catmull-Rom Curves

Catmull-Rom curves are a type of curve used in computer graphics and animation. They are defined by a set of control points and are known for their smooth and natural-looking shape. Catmull-Rom curves are used in various applications, from designing characters and objects to creating realistic motion paths. They are easy to compute and can be used in real-time applications, making them a popular choice among animators and game developers.

📝 Note: When working with curves, it's essential to consider the mathematical equations that define them, as well as the computational methods used to render them.

To summarize, curves are a fundamental aspect of design, architecture, and data analysis. By understanding the different types of curves and their applications, designers, engineers, and analysts can create innovative and informative representations that capture the essence of real-world phenomena. Whether it’s a Bezier curve, a spline curve, or an elliptical curve, each type of curve has its unique properties and benefits, making them an essential tool in various fields.