5 Ways To Find Probability

Introduction to Probability

The concept of probability is a fundamental aspect of mathematics and statistics, dealing with the likelihood of an event occurring. It is a measure of the chance or probability of an event happening, and it is expressed as a numerical value between 0 and 1. Probability is crucial in various fields, including insurance, finance, engineering, and social sciences. In this blog post, we will explore five ways to find probability, including the concept of probability, types of probability, and methods for calculating probability.

Understanding the Concept of Probability

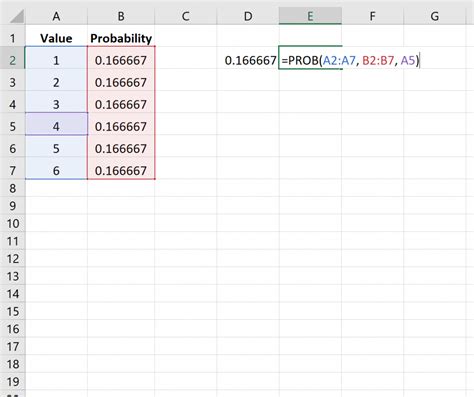
Before diving into the methods for finding probability, it’s essential to understand the concept of probability. Probability is defined as the number of favorable outcomes divided by the total number of possible outcomes. For example, if we flip a coin, there are two possible outcomes: heads or tails. If we want to find the probability of getting heads, we would divide the number of favorable outcomes (1) by the total number of possible outcomes (2), resulting in a probability of ¹⁄₂ or 0.5.

Types of Probability

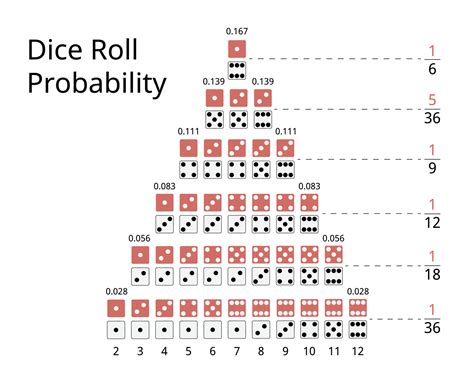
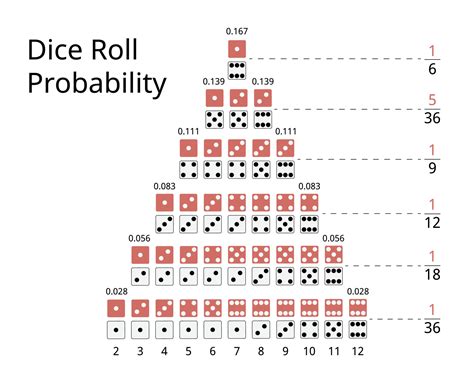
There are two main types of probability: theoretical probability and experimental probability. Theoretical probability is based on the number of favorable outcomes divided by the total number of possible outcomes, as mentioned earlier. Experimental probability, on the other hand, is based on repeated trials or experiments. For instance, if we conduct an experiment where we flip a coin 100 times and get heads 55 times, the experimental probability of getting heads would be ⁵⁵⁄₁₀₀ or 0.55.

5 Ways to Find Probability

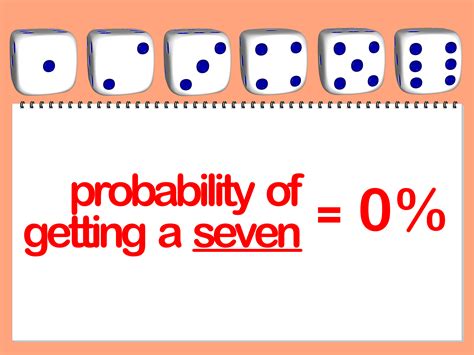
Now that we have a basic understanding of probability, let’s explore five ways to find probability: * Classical Probability: This method involves finding the probability of an event by dividing the number of favorable outcomes by the total number of possible outcomes. For example, if we roll a die, there are six possible outcomes: 1, 2, 3, 4, 5, and 6. If we want to find the probability of rolling a 3, we would divide the number of favorable outcomes (1) by the total number of possible outcomes (6), resulting in a probability of ¹⁄₆ or 0.17. * Relative Frequency: This method involves finding the probability of an event by dividing the number of times the event occurs by the total number of trials. For example, if we conduct an experiment where we roll a die 100 times and get a 3 twenty times, the relative frequency probability of rolling a 3 would be ²⁰⁄₁₀₀ or 0.2. * Subjective Probability: This method involves finding the probability of an event based on personal judgment or intuition. For example, if we ask someone to estimate the probability of it raining tomorrow, they might give a subjective probability of 0.7 based on their personal experience and weather forecast. * Empirical Probability: This method involves finding the probability of an event based on historical data or past experiences. For example, if we analyze the weather data for the past ten years and find that it rained on 70% of the days, the empirical probability of it raining tomorrow would be 0.7. * Tree Diagrams: This method involves using a visual representation to find the probability of an event. For example, if we want to find the probability of getting heads or tails when flipping two coins, we can use a tree diagram to illustrate the possible outcomes and calculate the probability of each outcome.

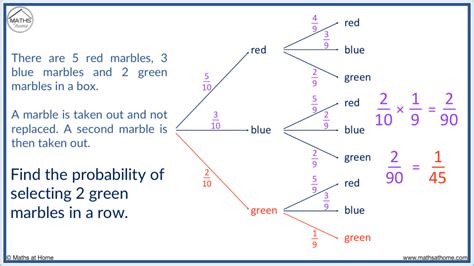
Calculating Probability Using Tree Diagrams

Tree diagrams are a useful tool for calculating probability, especially when dealing with multiple events. Here’s an example of how to use a tree diagram to calculate the probability of getting heads or tails when flipping two coins:

Event	Probability
Heads-Heads	0.25
Heads-Tails	0.25
Tails-Heads	0.25
Tails-Tails	0.25

Using the tree diagram, we can calculate the probability of getting heads or tails by adding the probabilities of each outcome.

📝 Note: When calculating probability using tree diagrams, it's essential to consider all possible outcomes and calculate the probability of each outcome.

To summarize, finding probability involves understanding the concept of probability, types of probability, and methods for calculating probability. The five ways to find probability discussed in this post include classical probability, relative frequency, subjective probability, empirical probability, and tree diagrams. By using these methods, we can calculate the probability of an event and make informed decisions.

As we reflect on the key points discussed, it’s clear that probability plays a vital role in various aspects of life, from insurance and finance to engineering and social sciences. By understanding the different methods for finding probability, we can better navigate the uncertainties of life and make more informed decisions. The concept of probability is complex and multifaceted, and there’s always more to learn and discover. Whether you’re a student, researcher, or professional, probability is an essential tool for analyzing data, making predictions, and understanding the world around us.