5 Ways Find Base Area

Introduction to Base Area Calculations

The base area of a shape or object is a fundamental concept in geometry and mathematics, crucial for understanding volume, surface area, and other properties. Calculating the base area can be straightforward for simple shapes like rectangles and triangles but can become complex for more intricate forms. This article explores five primary methods to find the base area of various shapes, emphasizing the importance of accurate calculations in real-world applications.
Understanding Base Area

Before diving into the calculation methods, it’s essential to understand what the base area represents. The base area is the area of the base of a three-dimensional shape. For a pyramid, it’s the area of the polygonal base, while for a cylinder, it’s the area of the circular base. The formula for calculating the base area varies depending on the shape of the base.
Method 1: Calculating the Base Area of a Rectangle

For a rectangular base, the calculation is straightforward. The formula for the area of a rectangle is length × width. This applies to any shape with a rectangular base, such as a rectangular prism or a cuboid.
Method 2: Calculating the Base Area of a Triangle
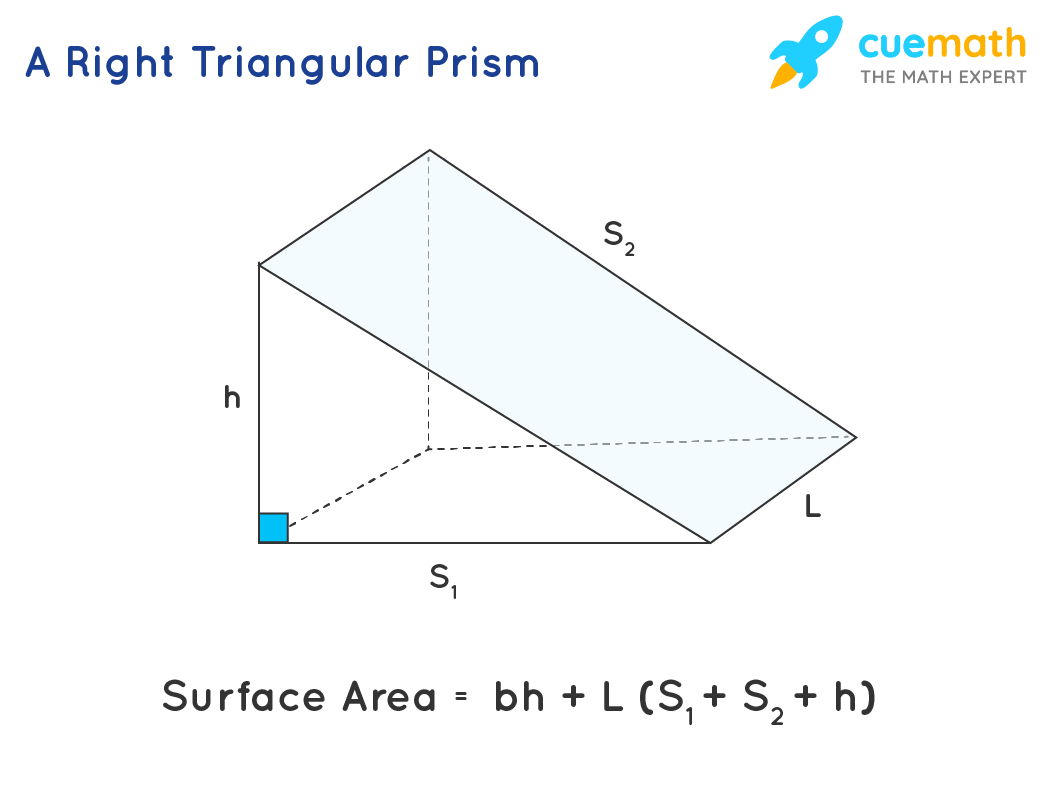
The base area of a triangular base, found in shapes like triangular prisms or pyramids, is calculated using the formula ½ × base × height. Here, the “base” refers to the length of one side of the triangle, and the “height” is the perpendicular distance from that base to the opposite vertex.
Method 3: Calculating the Base Area of a Circle

For shapes with a circular base, like cylinders or cones, the base area is calculated using the formula π × radius², where π (pi) is approximately 3.14159, and radius is the distance from the center of the circle to its edge.
Method 4: Calculating the Base Area of Complex Shapes

Complex shapes, such as those with irregular bases, require a different approach. One method involves dividing the shape into simpler components (like triangles or rectangles) and then summing their areas. Another approach is using the Shoelace formula for polygons, which calculates the area based on the coordinates of the vertices.
Method 5: Using Integration for Irregular Shapes

For shapes that cannot be easily divided into simpler forms, integration can be used to find the base area. This method involves defining the shape as a function and then integrating that function over the desired interval. While more complex, this method provides a powerful tool for calculating areas of highly irregular shapes.
📝 Note: The choice of method depends on the shape's complexity and the information available. For practical applications, especially in fields like architecture or engineering, accurate base area calculations are critical for designing stable and efficient structures.
In practical scenarios, understanding and applying these methods can significantly impact the success of projects. For instance, in construction, the base area of a building’s foundation affects its stability and the materials needed. In product design, the base area of a container influences its volume and the amount of material required for its production.
To illustrate the application of these methods, consider a simple example:
| Shape | Base Area Formula | Example Calculation |
|---|---|---|
| Rectangle | Length × Width | 10 cm × 5 cm = 50 cm² |
| Triangle | ½ × Base × Height | ½ × 6 cm × 8 cm = 24 cm² |
| Circle | π × Radius² | π × (4 cm)² = approximately 50.27 cm² |

Some key points to remember when calculating base areas include: - Accuracy: Ensure that measurements are precise to avoid calculation errors. - Formula Selection: Choose the correct formula based on the shape of the base. - Unit Consistency: Maintain consistent units throughout calculations to avoid conversion errors.
In summary, calculating the base area is a fundamental skill that requires understanding the geometric properties of shapes and applying the appropriate formulas. Whether dealing with simple geometric shapes or complex irregular forms, the ability to accurately calculate base areas is essential for a wide range of applications.
To further assist with understanding and applying these concepts, the following FAQs provide additional insights:
What is the base area, and why is it important?

+
The base area is the area of the base of a shape. It's crucial for calculating volumes, understanding structural integrity, and determining material requirements in various applications.
How do I calculate the base area of a complex shape?

+
For complex shapes, you can divide them into simpler shapes like triangles or rectangles and sum their areas. Alternatively, use the Shoelace formula for polygons or integration for highly irregular shapes.
What are common mistakes to avoid when calculating base areas?

+
Common mistakes include using the wrong formula for the shape, inconsistent units, and incorrect measurements. Double-checking calculations and ensuring accuracy in measurements can help avoid these mistakes.
The ability to calculate base areas accurately is a critical skill in mathematics and real-world applications, influencing the design, construction, and functionality of various objects and structures. By understanding and applying the appropriate methods for calculating base areas, individuals can enhance their problem-solving capabilities and contribute to more efficient and effective solutions in their respective fields.