5 Ways Calculate Slope Uncertainty

Introduction to Slope Uncertainty

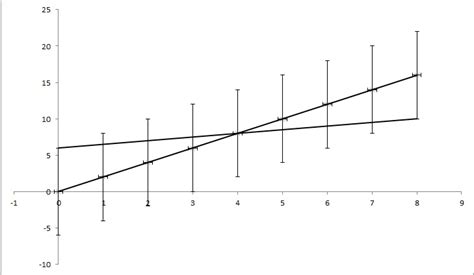
Calculating slope uncertainty is a critical aspect of various fields, including geography, engineering, and environmental science. Slope uncertainty refers to the error or uncertainty associated with the calculation of a slope, which can be due to various factors such as data quality, measurement errors, or model assumptions. In this blog post, we will discuss five ways to calculate slope uncertainty, highlighting the importance of each method and providing examples of their applications.

Method 1: Linear Regression

Linear regression is a widely used method for calculating slope uncertainty. This method involves fitting a linear model to a set of data points and estimating the slope and intercept of the line. The uncertainty of the slope can be calculated using the standard error of the slope, which takes into account the variability of the data points and the number of observations. Linear regression is a simple and effective method for calculating slope uncertainty, but it assumes a linear relationship between the variables, which may not always be the case.

Method 2: Bootstrapping

Bootstrapping is a resampling method that involves randomly selecting a subset of data points with replacement and calculating the slope for each subset. The bootstrap distribution of slopes can be used to estimate the uncertainty of the slope. Bootstrapping is a useful method for calculating slope uncertainty when the data is limited or when the relationship between the variables is complex. However, it can be computationally intensive and may require a large number of iterations to achieve stable results.

Method 3: Monte Carlo Simulation

Monte Carlo simulation is a method that involves generating random samples from a probability distribution and calculating the slope for each sample. The Monte Carlo distribution of slopes can be used to estimate the uncertainty of the slope. Monte Carlo simulation is a useful method for calculating slope uncertainty when the data is complex or when the relationship between the variables is non-linear. However, it can be computationally intensive and may require a large number of simulations to achieve stable results.

Method 4: Geostatistical Methods

Geostatistical methods, such as kriging, can be used to calculate slope uncertainty by accounting for the spatial autocorrelation of the data. These methods involve modeling the spatial relationship between the data points and estimating the slope and uncertainty of the slope at unsampled locations. Geostatistical methods are useful for calculating slope uncertainty in environmental and geological applications, where the data is often spatially correlated.

Method 5: Bayesian Methods

Bayesian methods, such as Bayesian linear regression, can be used to calculate slope uncertainty by accounting for prior knowledge and uncertainty. These methods involve updating the prior distribution with the observed data to obtain a posterior distribution of the slope and uncertainty of the slope. Bayesian methods are useful for calculating slope uncertainty when there is prior knowledge or uncertainty about the relationship between the variables.

📝 Note: The choice of method for calculating slope uncertainty depends on the nature of the data, the complexity of the relationship between the variables, and the level of uncertainty associated with the data.

The following table summarizes the five methods for calculating slope uncertainty:

Method	Description	Advantages	Disadvantages
Linear Regression	Linear model fitting	Simple, effective	Assumes linear relationship
Bootstrapping	Resampling method	Useful for complex relationships	Computationally intensive
Monte Carlo Simulation	Random sampling	Useful for complex relationships	Computationally intensive
Geostatistical Methods	Spatial modeling	Useful for spatially correlated data	Requires spatial data
Bayesian Methods	Prior knowledge updating	Useful for prior knowledge or uncertainty	Requires prior knowledge

In summary, calculating slope uncertainty is a critical aspect of various fields, and there are several methods available for doing so. The choice of method depends on the nature of the data, the complexity of the relationship between the variables, and the level of uncertainty associated with the data. By understanding the advantages and disadvantages of each method, researchers and practitioners can select the most appropriate method for their specific application.