5 Key Hardy Weinberg Answers Unveiled

The Hardy-Weinberg principle is a cornerstone of population genetics, providing a mathematical model that describes the genetic variation in a population. For those fascinated by how genes spread and evolve within populations, understanding the Hardy-Weinberg equilibrium is not just enlightening but also essential for further studies in genetics. This post unveils five key answers related to the Hardy-Weinberg principle, detailing how it applies in real-world scenarios, its limitations, and how it aids in genetic research.
What is the Hardy-Weinberg Principle?

The Hardy-Weinberg principle, sometimes known as the Hardy-Weinberg equilibrium (HWE), states that allele and genotype frequencies in a population will remain constant from generation to generation in the absence of other evolutionary influences. This principle was independently proposed by G. H. Hardy, an English mathematician, and Wilhelm Weinberg, a German physician, in 1908.
To understand this principle, consider the following:
- Allele Frequency: The frequency of an allele in a population.
- Genotype Frequency: The frequency of a particular combination of alleles in individuals of the population.
Here are the key assumptions of the Hardy-Weinberg principle:
- No mutations
- No gene flow (migration into or out of the population)
- No selection
- No random mating (individuals mate randomly with respect to the gene in question)
- Very large population size (to avoid genetic drift)
Mathematical Basis of the Principle
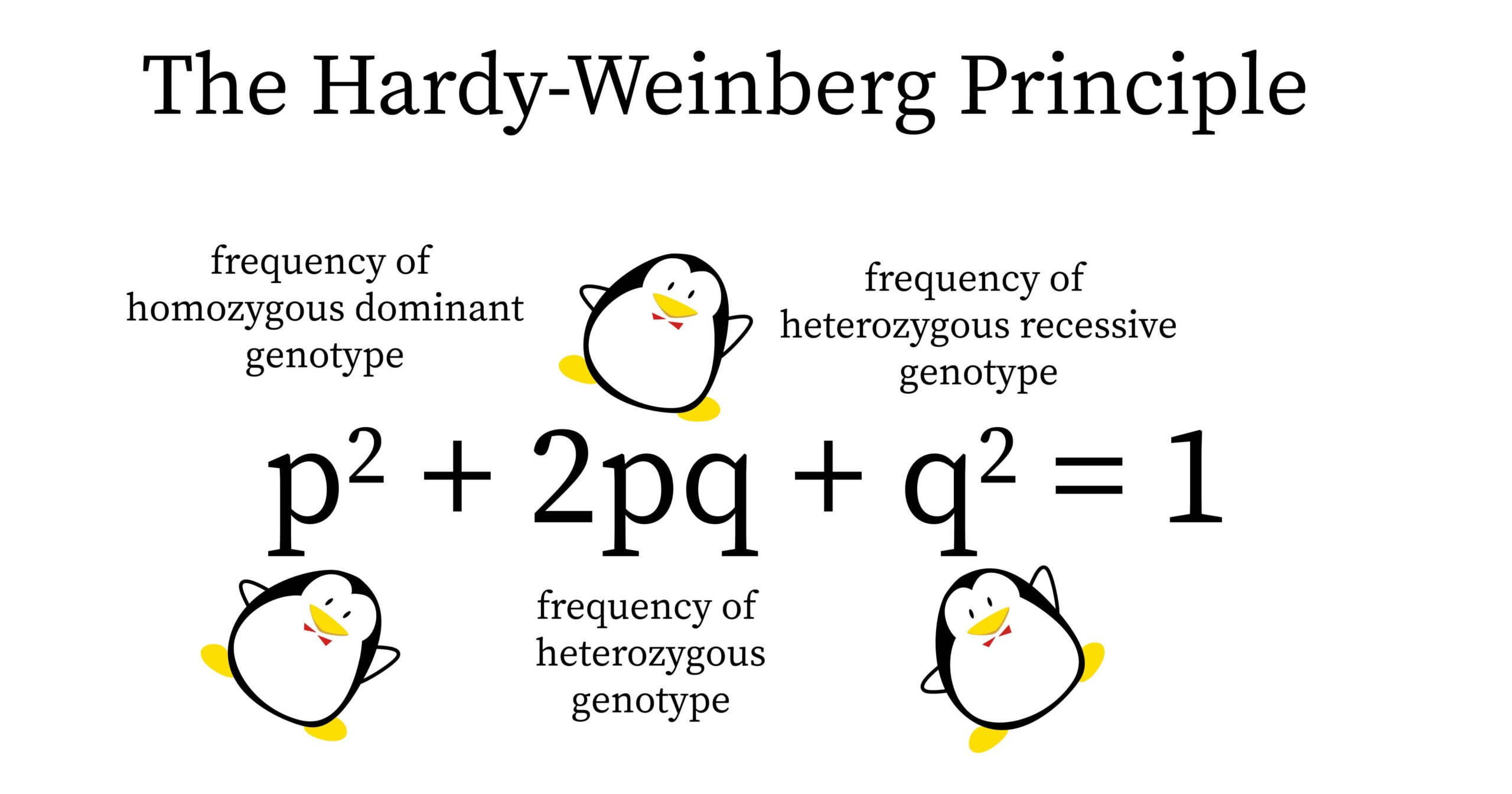
Let's delve into the math behind this principle. Suppose there are two alleles of a particular gene, say A and a, in a population. The frequency of the A allele is p, and that of the a allele is q. By definition, p + q = 1.
The HWE equation can be expressed as:
\[p^2 + 2pq + q^2 = 1\]Where:
- p2 represents the frequency of the AA genotype
- 2pq represents the frequency of the Aa heterozygotes
- q2 represents the frequency of the aa genotype
Application in Real World

The Hardy-Weinberg principle provides a baseline to detect evolutionary processes:
- It serves as a null hypothesis against which changes in population genetics can be tested.
- Discrepancies from HWE suggest evolution is occurring through one of the five mechanisms (mutation, gene flow, selection, non-random mating, genetic drift).
- In medical genetics, it helps calculate carrier frequencies for genetic disorders.
- Ecologists use it to understand population structure and to assess the impact of conservation strategies on genetic diversity.
Limitations of Hardy-Weinberg

While the Hardy-Weinberg principle offers a clear framework, it does not often reflect real-world populations:
- Real populations are influenced by evolutionary factors, making deviations from HWE common.
- The assumptions are rarely met in natural populations, leading to potential misinterpretation of results.
- Small sample sizes can lead to inaccurate estimations of allele frequencies, impacting the model's accuracy.
📌 Note: When applying the Hardy-Weinberg principle, it's essential to recognize its idealized nature and use it as a tool for understanding, not as an exact mirror of natural genetic behavior.
Extensions and Modifications

Over the years, several modifications and extensions have been proposed to make the principle more applicable to real-world scenarios:
- F-statistics: These statistics help quantify the effects of subpopulations and inbreeding, adjusting the Hardy-Weinberg model for more complex population structures.
- Multiallelic Systems: Extending the model to include more than two alleles, providing a broader analysis of genetic variation.
- Linkage Disequilibrium: Exploring how closely genes are associated and how this affects the distribution of alleles.
The Hardy-Weinberg principle, though simple in its core idea, remains one of the most effective tools for understanding and analyzing population genetics. By providing a snapshot of what a non-evolving population would look like, it offers a clear benchmark to measure evolutionary changes. As we delve deeper into genetic research, the principle's application continues to grow, adapting to new insights and the complexities of biological systems. Its ability to highlight deviations from the norm allows scientists to identify and study evolutionary forces at work, enriching our understanding of the intricate dance between genetics and evolution.
Why is the Hardy-Weinberg principle important for genetic studies?

+
The principle helps geneticists identify deviations from expected allele frequencies, which can indicate evolutionary processes or genetic disorders. It’s a fundamental tool for assessing how a population is changing genetically over time.
Can the Hardy-Weinberg model be applied to small populations?

+
While the model assumes infinite population size, small populations can be analyzed using Hardy-Weinberg to approximate genetic structure, though adjustments must be made for genetic drift which is more significant in small populations.
How does non-random mating affect Hardy-Weinberg equilibrium?

+
Non-random mating can lead to changes in genotype frequencies, causing deviations from Hardy-Weinberg equilibrium due to assortative mating (like with like) or disassortative mating (unlike with unlike). This is often reflected in inbreeding coefficients.