Graphing Quadratic Functions Made Easy with Worksheets
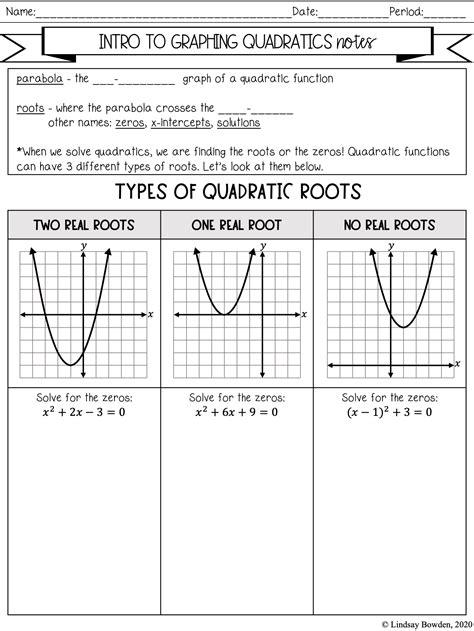
Understanding Quadratic Functions

Quadratic functions are a fundamental concept in algebra, and graphing them is an essential skill for any student to master. A quadratic function is a polynomial function of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic function is f(x) = ax^2 + bx + c, where a, b, and c are constants.
The Importance of Graphing Quadratic Functions
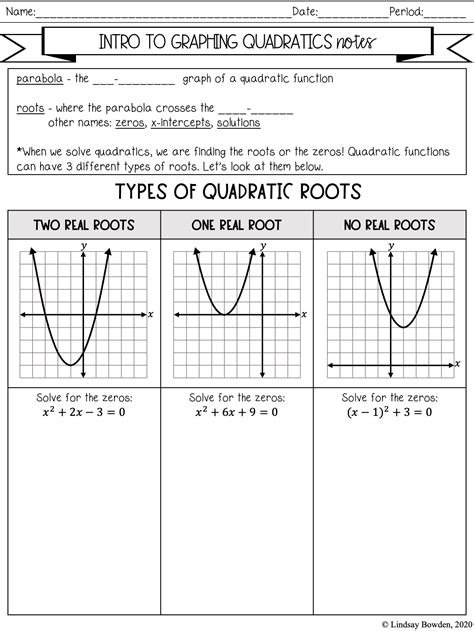
Graphing quadratic functions is crucial because it helps visualize the relationship between the function and its input values. By analyzing the graph, you can identify key features such as the vertex, axis of symmetry, and x-intercepts. These features are essential in solving problems involving quadratic functions.
Benefits of Using Worksheets for Graphing Quadratic Functions
Worksheets are an excellent tool for learning to graph quadratic functions. They provide a structured approach to learning, allowing students to practice and reinforce their understanding of the concept. Here are some benefits of using worksheets for graphing quadratic functions:
• Improved understanding: Worksheets help students develop a deeper understanding of quadratic functions and their graphs. • Practice and reinforcement: Worksheets provide ample opportunities for students to practice graphing quadratic functions, reinforcing their learning. • Development of problem-solving skills: Worksheets challenge students to apply their knowledge of quadratic functions to solve problems.
A Step-by-Step Guide to Graphing Quadratic Functions

Graphing quadratic functions can seem daunting, but with a step-by-step approach, it becomes more manageable. Here’s a step-by-step guide to graphing quadratic functions:
- Write the function in standard form: Ensure the function is in the form f(x) = ax^2 + bx + c.
- Identify the vertex: The vertex is the minimum or maximum point on the graph. Use the formula x = -b/2a to find the x-coordinate of the vertex.
- Determine the axis of symmetry: The axis of symmetry is the vertical line that passes through the vertex. Use the formula x = -b/2a to find the equation of the axis of symmetry.
- Find the x-intercepts: The x-intercepts are the points where the graph crosses the x-axis. Use the quadratic formula x = (-b ± √(b^2 - 4ac)) / 2a to find the x-intercepts.
- Plot the points: Plot the vertex, axis of symmetry, and x-intercepts on the coordinate plane.
- Draw the graph: Use the plotted points to draw the graph of the quadratic function.
📝 Note: When graphing quadratic functions, it's essential to label the axis of symmetry and vertex clearly.
Example: Graphing a Quadratic Function
Let’s graph the quadratic function f(x) = x^2 + 4x + 4.
- Write the function in standard form: f(x) = x^2 + 4x + 4
- Identify the vertex: x = -b/2a = -4⁄2(1) = -2
- Determine the axis of symmetry: x = -b/2a = -4⁄2(1) = -2
- Find the x-intercepts: x = (-b ± √(b^2 - 4ac)) / 2a = (-4 ± √(4^2 - 4(1)(4))) / 2(1) = -2 ± √0 = -2
- Plot the points: Plot the vertex (-2, 0), axis of symmetry x = -2, and x-intercept (-2, 0) on the coordinate plane.
- Draw the graph: Use the plotted points to draw the graph of the quadratic function.
Worksheets for Graphing Quadratic Functions

Worksheets are an excellent resource for practicing graphing quadratic functions. Here’s an example worksheet:
| Function | Vertex | Axis of Symmetry | X-Intercepts |
|---|---|---|---|
| f(x) = x^2 + 4x + 4 | (-2, 0) | x = -2 | (-2, 0) |
| f(x) = x^2 - 4x - 3 | (2, -1) | x = 2 | (3, 0), (-1, 0) |
| f(x) = x^2 + 2x - 6 | (-1, -7) | x = -1 | (-3, 0), (2, 0) |

📝 Note: You can create your own worksheets using the steps outlined above.
Conclusion

Graphing quadratic functions is an essential skill in algebra, and worksheets can help make the process more manageable. By following the step-by-step guide and practicing with worksheets, you can develop a deeper understanding of quadratic functions and their graphs.
What is the general form of a quadratic function?

+
The general form of a quadratic function is f(x) = ax^2 + bx + c, where a, b, and c are constants.
How do I find the vertex of a quadratic function?
+
The vertex is the minimum or maximum point on the graph. Use the formula x = -b/2a to find the x-coordinate of the vertex.
What is the axis of symmetry in a quadratic function?

+
The axis of symmetry is the vertical line that passes through the vertex. Use the formula x = -b/2a to find the equation of the axis of symmetry.
Related Terms:
- Desmos
- GeoGebra
- Symbolab
- Photomath
- Microsoft Math Solver
- Wolfram Alpha