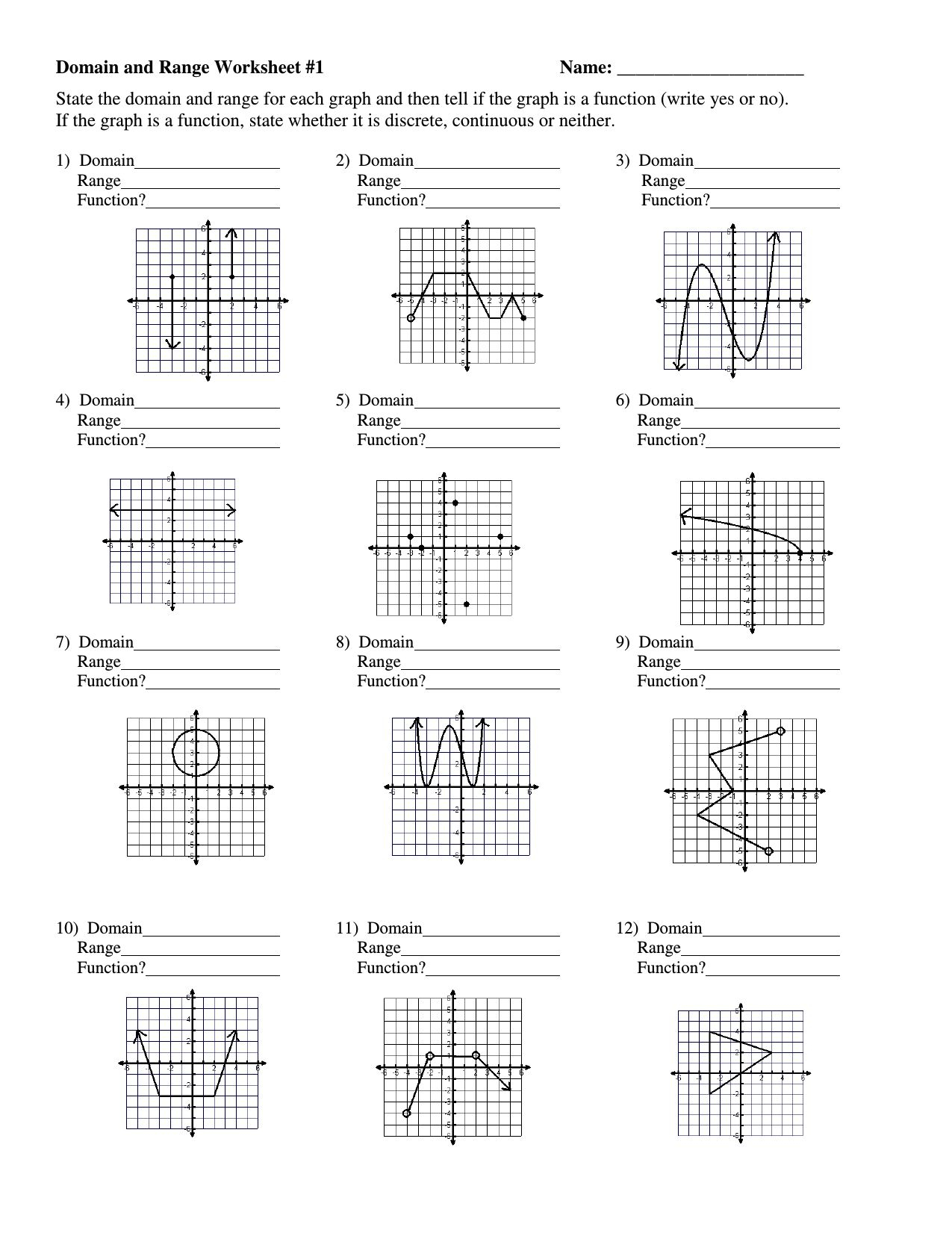
Graphing Rational Functions: Ultimate Worksheet Guide

If you're learning or teaching algebra, understanding and graphing rational functions can seem daunting at first. Rational functions, defined as ratios of polynomial functions, present unique behaviors like vertical asymptotes, horizontal asymptotes, and holes, which make them particularly interesting. This guide will walk you through the process of graphing rational functions, providing you with a comprehensive worksheet guide to master this topic.
Understanding Rational Functions

A rational function can be expressed in the form:
[ f(x) = \frac{P(x)}{Q(x)} ]
where ( P(x) ) and ( Q(x) ) are polynomials, and ( Q(x) \neq 0 ).
- Vertical Asymptotes: Occur where the denominator equals zero, provided the numerator is not zero at these points.
- Horizontal Asymptotes: Depend on the degrees of the polynomials in the numerator and denominator.
- Holes: Found where both numerator and denominator are zero simultaneously.
📝 Note: Always ensure your function is in its simplest form before graphing; factor both the numerator and the denominator.
Steps to Graph Rational Functions

1. Factor the Polynomials
First, factor both the numerator and the denominator. This step helps identify vertical asymptotes, holes, and simplifies the function:
[ f(x) = \frac{(x-2)(x+3)}{(x-1)^2(x+4)} ]
2. Identify Discontinuities

Determine where the function is undefined or has discontinuities:
- Vertical Asymptotes: From the denominator, you get x = 1 and x = -4 .
- Holes: If x - 2 = 0 in both numerator and denominator, there's a hole at x = 2 .
3. Analyze the Horizontal Asymptotes

Use the degrees of the polynomials in the numerator and denominator to find horizontal asymptotes:
| Degree of Numerator (m) | Degree of Denominator (n) | Horizontal Asymptote |
|---|---|---|
| m < n | y = 0 | |
| m = n | Compare the coefficients of the leading terms | |
| m > n | No horizontal asymptote, oblique asymptote instead |

4. Determine Oblique Asymptotes

If the degree of the numerator is greater, perform polynomial division to find the quotient, which gives you the oblique asymptote.
5. Plot Key Points
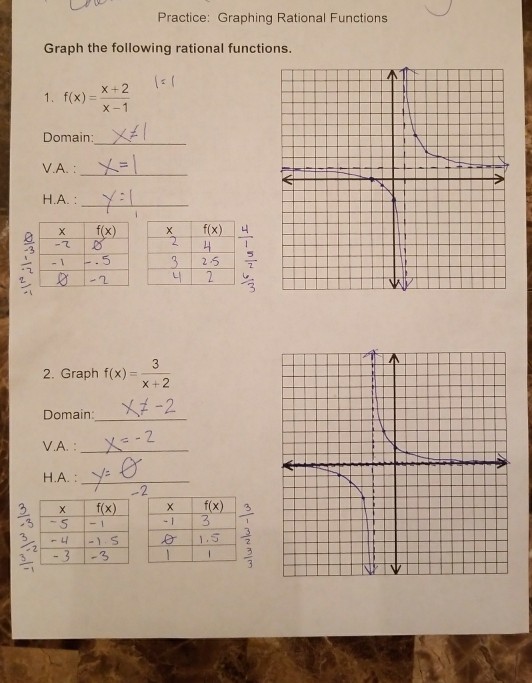
Choose x-values to find corresponding y-values, focusing on:
- x-intercepts (where numerator equals zero).
- Points near and on the other side of vertical asymptotes.
- The behavior as x approaches infinity or negative infinity.
6. Sketch the Graph

With all this information:
- Draw the vertical asymptotes.
- Draw the horizontal or oblique asymptote if any.
- Plot your points, holes, and the shape of the graph considering the behavior around asymptotes.
Here is an example graph for:
[ f(x) = \frac{(x-2)(x+3)}{(x-1)^2(x+4)} ]

📝 Note: The exact appearance of the graph can change based on the specific function; these steps provide a general framework.
Advanced Tips for Graphing Rational Functions

End Behavior

Understanding the end behavior helps you anticipate how the function behaves as x \to \pm\infty :
- If the degree of the denominator is higher, y \to 0 .
- If both degrees are equal, look at the leading coefficients for the asymptote's y-value.
Recognizing Transformations

Rational functions can have transformations like shifts, stretches, or reflections. Look for patterns in the coefficients and constants:
- Horizontal shifts: f(x - h) .
- Vertical shifts: f(x) + k .
- Reflections: If f(-x) or -f(x) .
📝 Note: Transformation analysis can significantly simplify the graphing process.
Final Thoughts

Graphing rational functions is a skill that becomes intuitive with practice. By understanding the steps outlined above, you can methodically approach any rational function and predict its behavior. Remember that each function has its own peculiarities, but the principles remain consistent. From identifying asymptotes to plotting key points, mastering these techniques will make graphing rational functions less of a challenge and more of an intriguing exploration into the beauty of algebraic functions.
How do I identify a hole in a rational function?

+
Identify factors that are common to both the numerator and the denominator. Cancel these factors out to find the holes at the resulting x-values.
What’s the difference between a vertical and horizontal asymptote?

+
Vertical asymptotes occur where the denominator is zero and the function heads towards ±∞. Horizontal asymptotes describe the end behavior as x approaches ±∞, indicating where the function stabilizes in terms of y-value.
Can rational functions have slant asymptotes?
+Yes, if the degree of the numerator is exactly one higher than the denominator, you’ll find a slant (or oblique) asymptote by performing polynomial long division.