Master Quadratic Graphs: Factored Form Worksheet Guide

Understanding Quadratic Equations

Quadratic equations are fundamental in algebra, often introduced early in a student’s mathematical journey. They are represented in various forms, but understanding the factored form is crucial for graphing and solving these equations. Factored form provides insight into the roots (x-intercepts) of the quadratic equation, making it easier to visualize and interpret the graph.
Why Factored Form?

The factored form of a quadratic equation, written as a(x - p)(x - q), where ‘a’ is a coefficient and ‘p’ and ‘q’ are the roots, directly tells us where the parabola will intersect the x-axis. This form is particularly useful because:
- It immediately shows the x-intercepts without needing to solve for them.
- It simplifies the process of sketching the parabola, as the roots give you key points on the graph.
- It helps in understanding the behavior of the parabola - whether it opens upwards or downwards based on the value of ‘a’.
How to Graph Quadratic Equations in Factored Form

Let’s dive into the step-by-step process of graphing a quadratic equation when it’s presented in its factored form:
Step 1: Identify the Roots

From the factored form a(x - p)(x - q), ‘p’ and ‘q’ are the x-intercepts or roots of the equation. Plot these points on the x-axis.
Step 2: Determine the Direction of Opening

The coefficient ‘a’ dictates whether the parabola opens upwards (if ‘a’ is positive) or downwards (if ‘a’ is negative). This helps in sketching the basic shape of the curve.
Step 3: Find the Vertex

The vertex of a parabola in factored form can be found using the midpoint formula between the roots:
- Vertex x-coordinate: (p + q) / 2
- To find the y-coordinate, substitute the x-coordinate back into the equation.
Step 4: Plot Additional Points

Now, plot a few more points to ensure accuracy:
- Choose points between the roots to confirm the shape near the axis of symmetry.
- Plot points outside the roots to define the extremities of the parabola.
Step 5: Sketch the Parabola

Connect the points in a smooth curve, ensuring the parabola reflects the direction of opening based on ‘a’ and passes through the vertex and the x-intercepts.
📝 Note: If you are given a quadratic equation not in factored form, you might need to factor it first or use other methods like completing the square or the quadratic formula to find the roots.
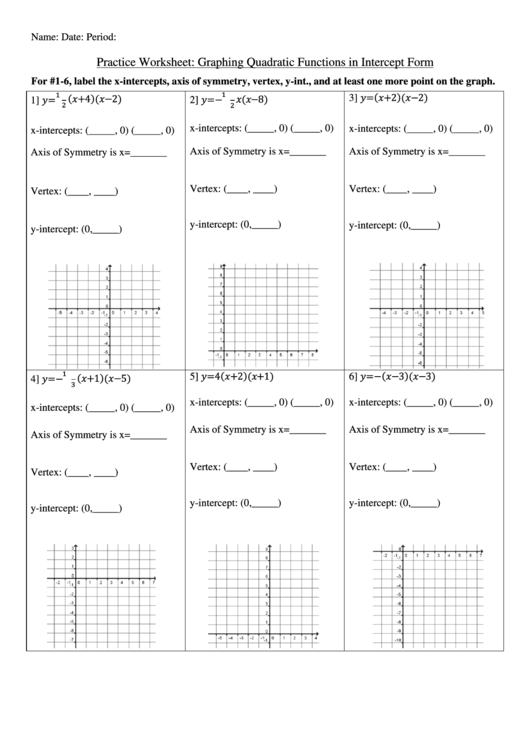
Factored Form Worksheet Guide

Here’s a guide on how you can structure a worksheet to practice quadratic graphing in factored form:
| Example | Roots | Vertex | Direction of Opening | Sketch |
|---|---|---|---|---|
| y = 3(x - 2)(x - 4) | x = 2, x = 4 | (3, -9) | Upwards | Draw an upward-facing parabola with roots at 2 and 4, and vertex at (3, -9). |
| y = -2(x + 1)(x - 3) | x = -1, x = 3 | (1, 4) | Downwards | Sketch a downward-facing parabola with roots at -1 and 3, and vertex at (1, 4). |

Include instructions for students to:
- Determine the roots of the given equations.
- Calculate the vertex coordinates.
- Decide the direction of the parabola.
- Sketch the graph on the provided coordinate plane.
📝 Note: Remind students to label axes, scales, and critical points on their sketches to improve understanding and clarity.
Through this process, students not only practice the mechanics of graphing quadratic functions but also enhance their conceptual understanding of how changes in coefficients affect the graph's behavior. This practice will solidify their ability to transition between different forms of quadratic equations and interpret them graphically.
This guide emphasizes the importance of visual representation in algebra, making abstract mathematical concepts more tangible and understandable. By mastering the graphing of quadratic equations in factored form, students gain confidence in their mathematical skills, paving the way for more advanced algebraic studies.
What is the advantage of using the factored form for quadratic equations?
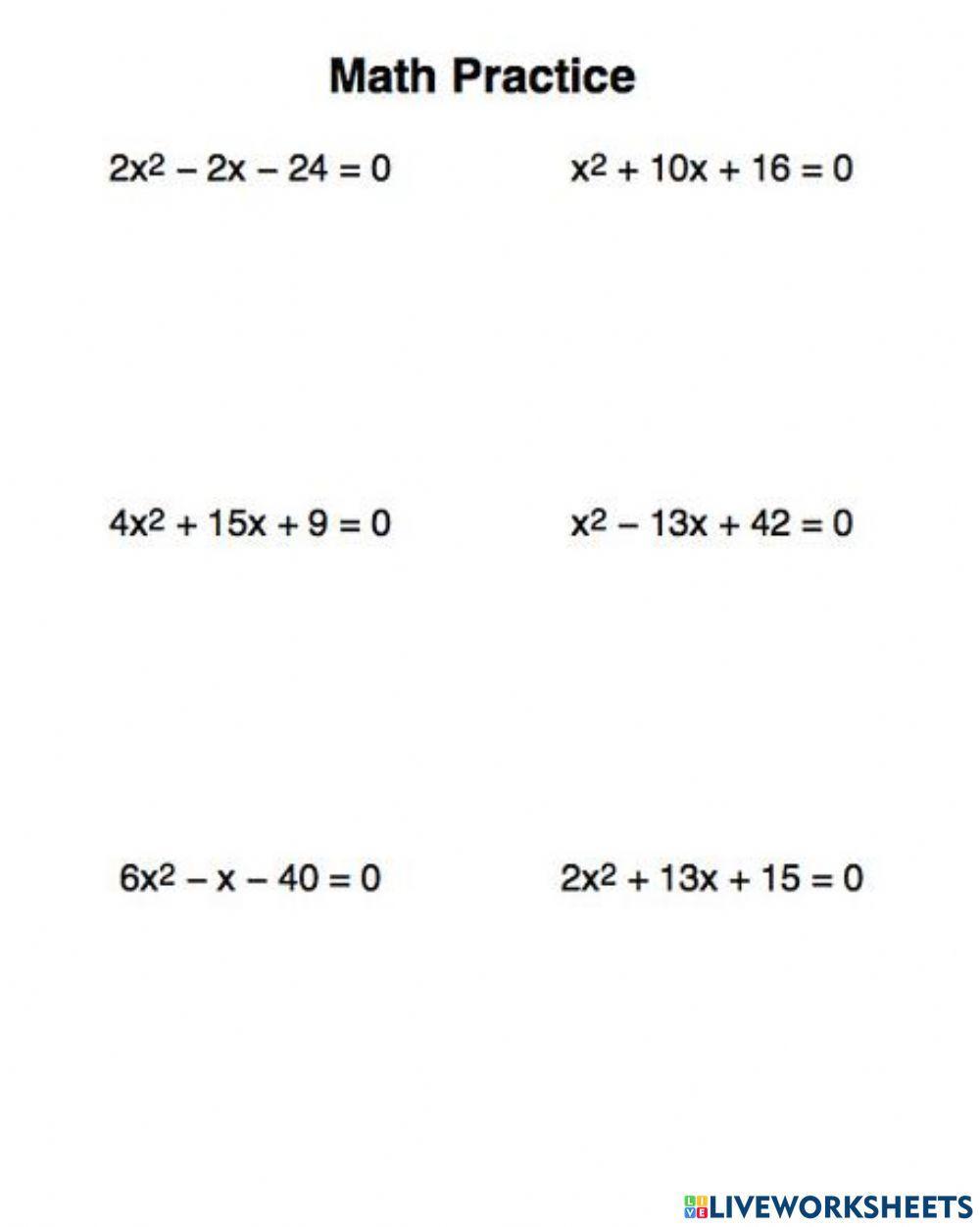
+
The factored form immediately provides the roots of the equation, which are critical points for sketching the graph. It also simplifies solving and interpreting the quadratic function graphically.
How do you find the vertex of a parabola given in factored form?
+
To find the vertex, calculate the midpoint between the roots: (p + q)/2, where p and q are the roots. Substitute this x-value back into the equation to find the corresponding y-value.
Can you graph a parabola with only one x-intercept?

+
Yes, in such cases, the equation might be in the form y = a(x - p)^2, indicating that the parabola touches the x-axis at one point, creating a double root. The vertex of the parabola will be at (p, 0).