Graphing Linear Inequalities: Shading Solutions Explained
The concept of graphing linear inequalities is essential for students and professionals alike, not just in mathematics, but across various fields where problem-solving, analytical skills, and decision-making are critical. Linear inequalities provide a foundation for understanding more complex mathematical relationships, optimizing solutions, and even in everyday applications such as scheduling, budgeting, or strategic planning.
Understanding Linear Inequalities
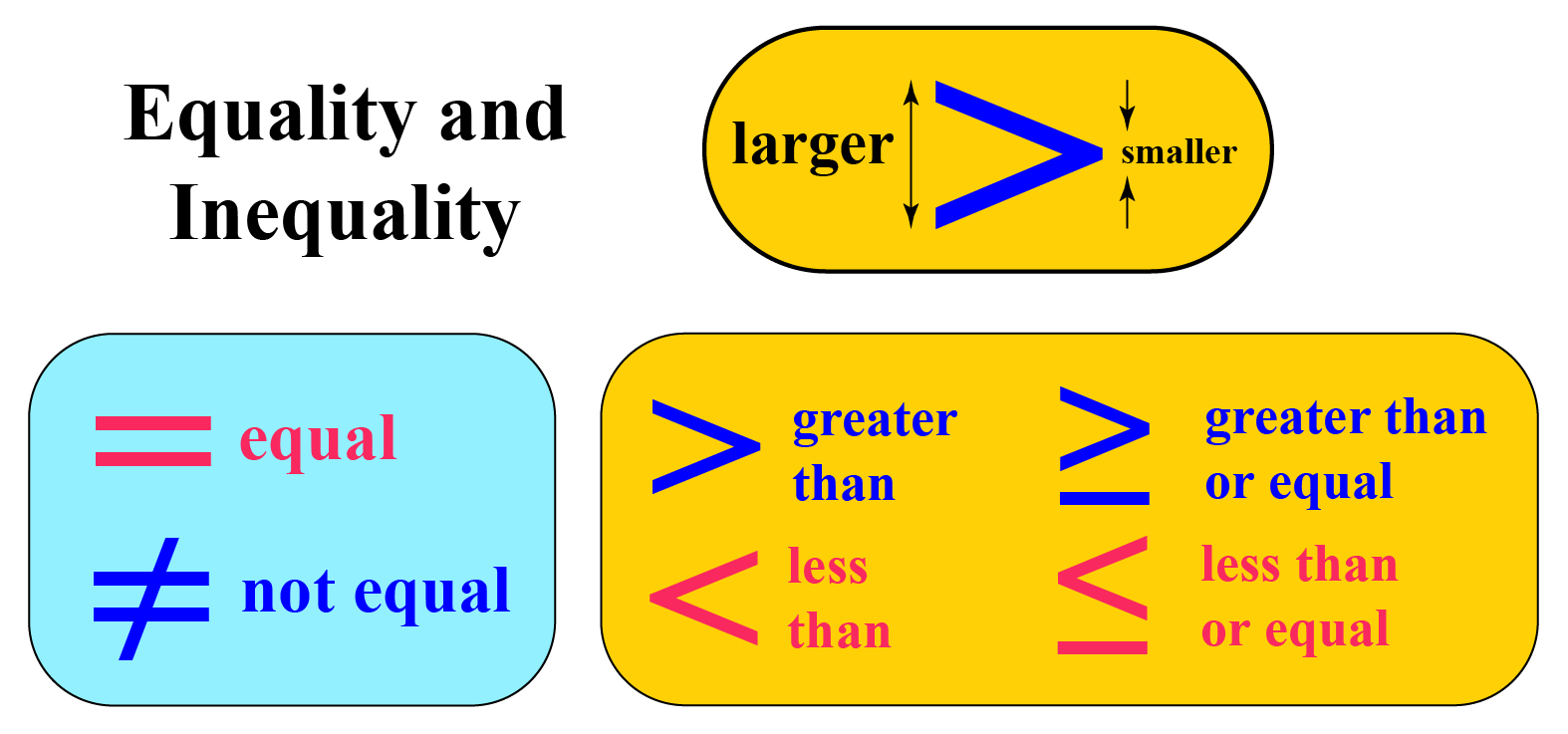
Linear inequalities differ from linear equations by introducing inequality symbols like <, >, ≤, or ≥ instead of the equals sign (=). These symbols represent relationships where one side might be greater than, less than, or equal to the other side. Understanding these symbols is crucial as they dictate the direction of the shading when graphing inequalities.
Basic Steps for Graphing Linear Inequalities

Graphing linear inequalities involves a series of steps that transform a mathematical expression into a visual representation:
- Step 1: Replace the Inequality with an Equation - Convert the inequality to an equation by replacing the inequality symbol with an equals sign. This helps in plotting the line.
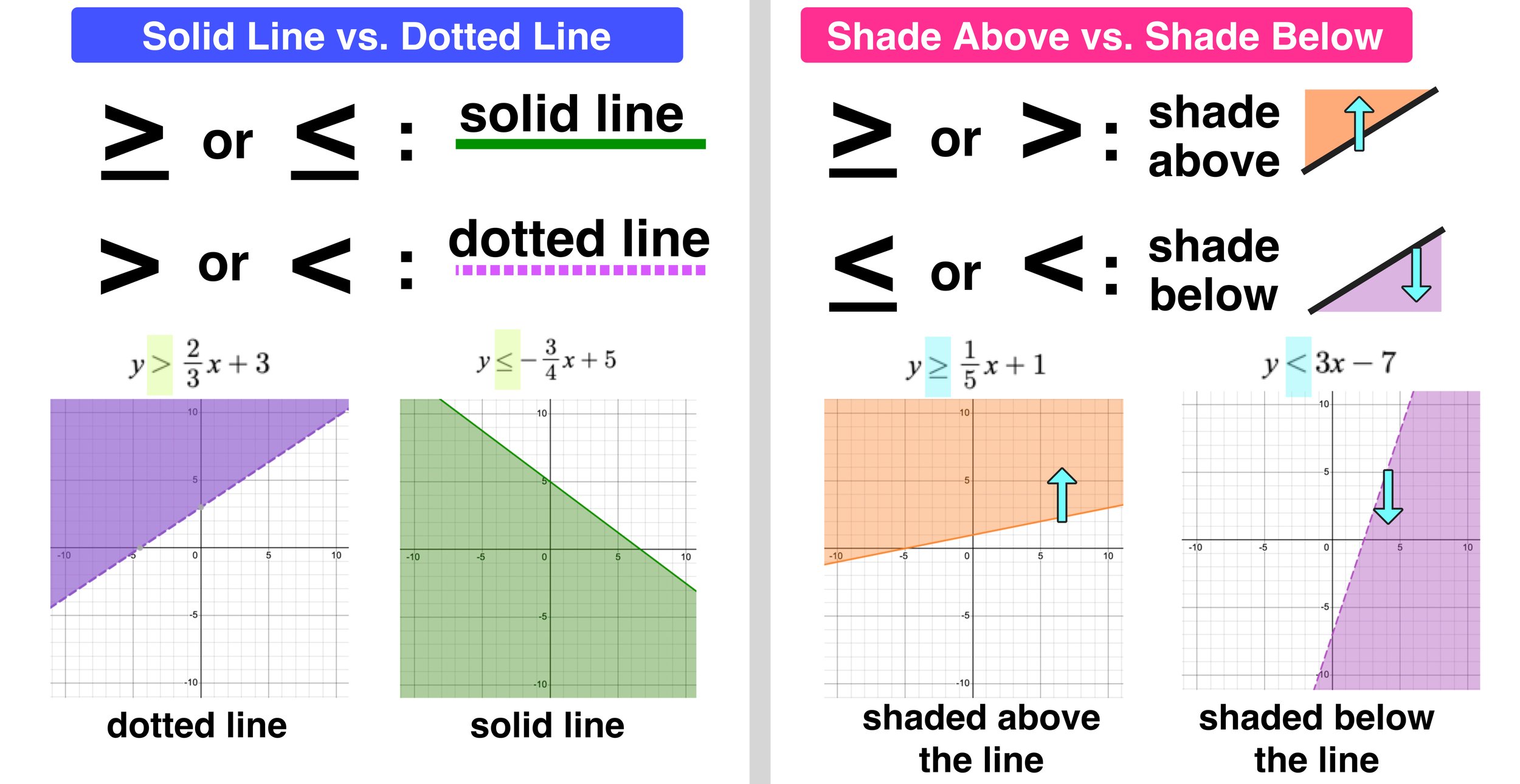
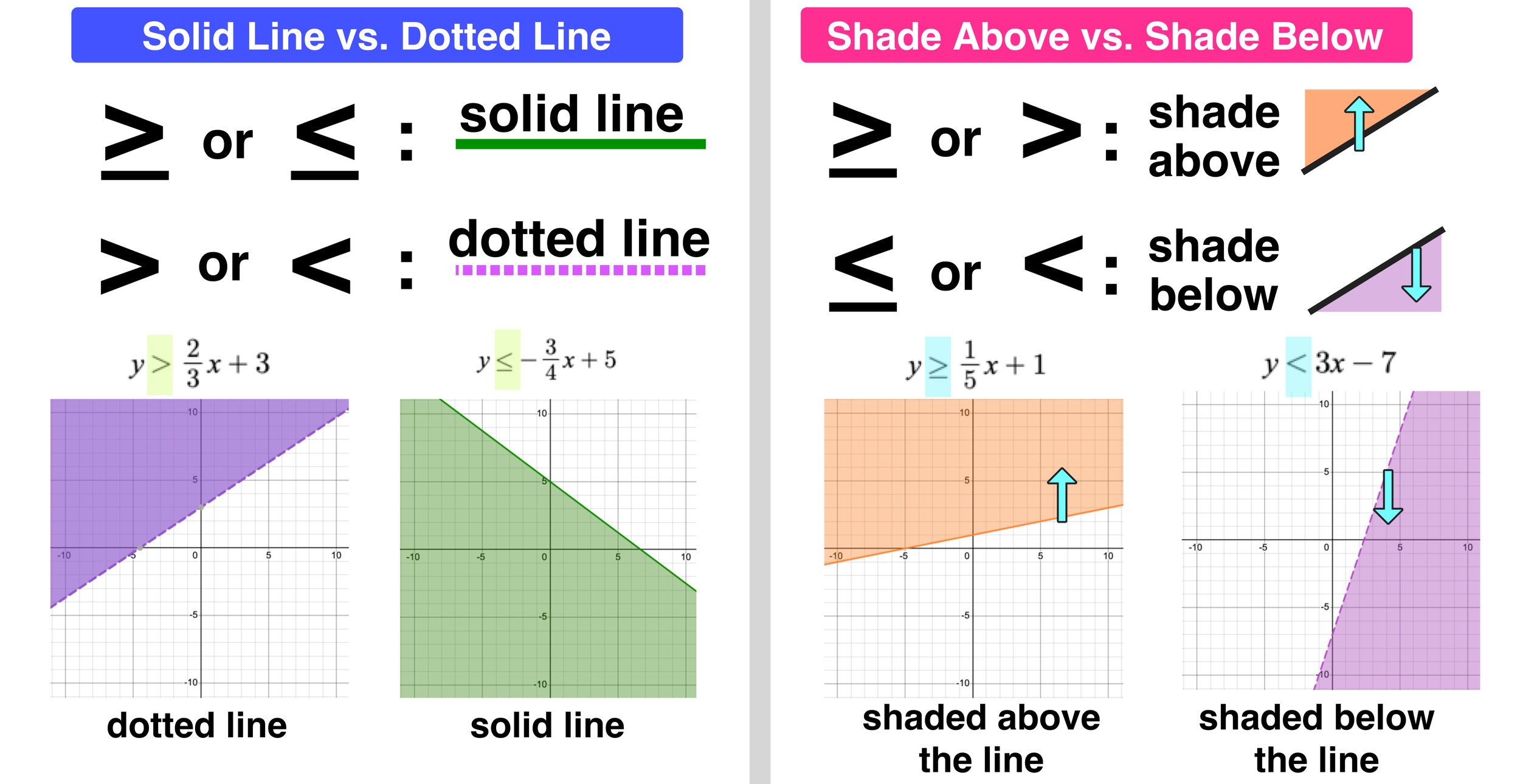
- Step 2: Graph the Line - Plot this equation on a coordinate plane. Use a solid line if the inequality includes ≤ or ≥, and a dashed line for < or >.
- Step 3: Choose a Test Point - Select a point not on the line to test which side to shade. If this point satisfies the inequality, shade the region containing this point. If not, shade the other side.
- Step 4: Shade the Region - Shade the half-plane that satisfies the inequality. Remember, for ‘or equal to’ inequalities, include the line in the shaded area.
- Step 5: Verify the Graph - Check your shading by using a few points within the shaded region to confirm they satisfy the inequality.
📚 Note: Always choose a test point that does not lie on the line to avoid ambiguity.
Graphing Multiple Inequalities
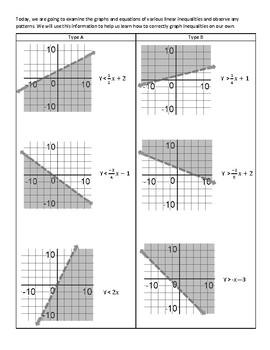
When dealing with systems of linear inequalities, the approach expands to include:
- Graph each inequality separately - Plot the boundary lines, choosing whether they are solid or dashed based on the inequality symbols.
- Find common areas - Identify the intersection or overlapping areas where all conditions are met simultaneously.
- Shade the common region - Shade this common region, which represents the solution set for all inequalities combined.
Applications and Importance of Linear Inequalities

Linear inequalities are not just abstract concepts but have practical applications:
- Optimization - They are used in linear programming to find optimal solutions under constraints.
- Economics - For modeling production or consumption limits.
- Engineering - In system design to ensure specifications are met within operational bounds.
- Education - As a fundamental concept in mathematics education, teaching logical thinking and problem-solving.
Now, let's look at some specific examples to illustrate how these steps are applied in real-world scenarios.
Example: Diet Planning

Consider a scenario where a nutritionist needs to plan a diet:
- Let’s say the diet requires at least 50 grams of protein but no more than 300 grams of carbohydrates per day.
- The equation for protein might look like P ≥ 50, and for carbohydrates, C ≤ 300.
- Graphing these inequalities, we would find the overlapping region where both conditions are satisfied, ensuring a balanced diet.
Wrapping Up

The process of graphing linear inequalities provides a visual interpretation of mathematical constraints, which is incredibly powerful for both learning and problem-solving. By breaking down inequalities into steps, shading solutions, and understanding how these shapes intersect, we can solve real-world problems efficiently. This method of solving not only aids in understanding mathematics but also in practical decision-making across different disciplines.
Whether for personal budgeting, resource allocation in business, or complex engineering design, the ability to graph and interpret linear inequalities allows for better strategic planning and optimization. The practice of using linear inequalities fosters logical thinking, helping one to navigate through the myriad of options available in decision-making scenarios.
Why do we use solid and dashed lines when graphing inequalities?

+
Solid lines are used when the inequality includes or equal to signs (≤ or ≥) because the line itself is part of the solution. Dashed lines are used for strict inequalities (< or >) to indicate the solution does not include points on the line.
How do you know which region to shade?
+
By choosing a test point not on the line, you can determine which side of the line satisfies the inequality. If the point satisfies the inequality, shade the region containing it; if not, shade the opposite side.
Can linear inequalities have more than one solution?

+
Yes, linear inequalities typically have an infinite number of solutions, which can be visualized as a region on the graph rather than a single point as with linear equations.