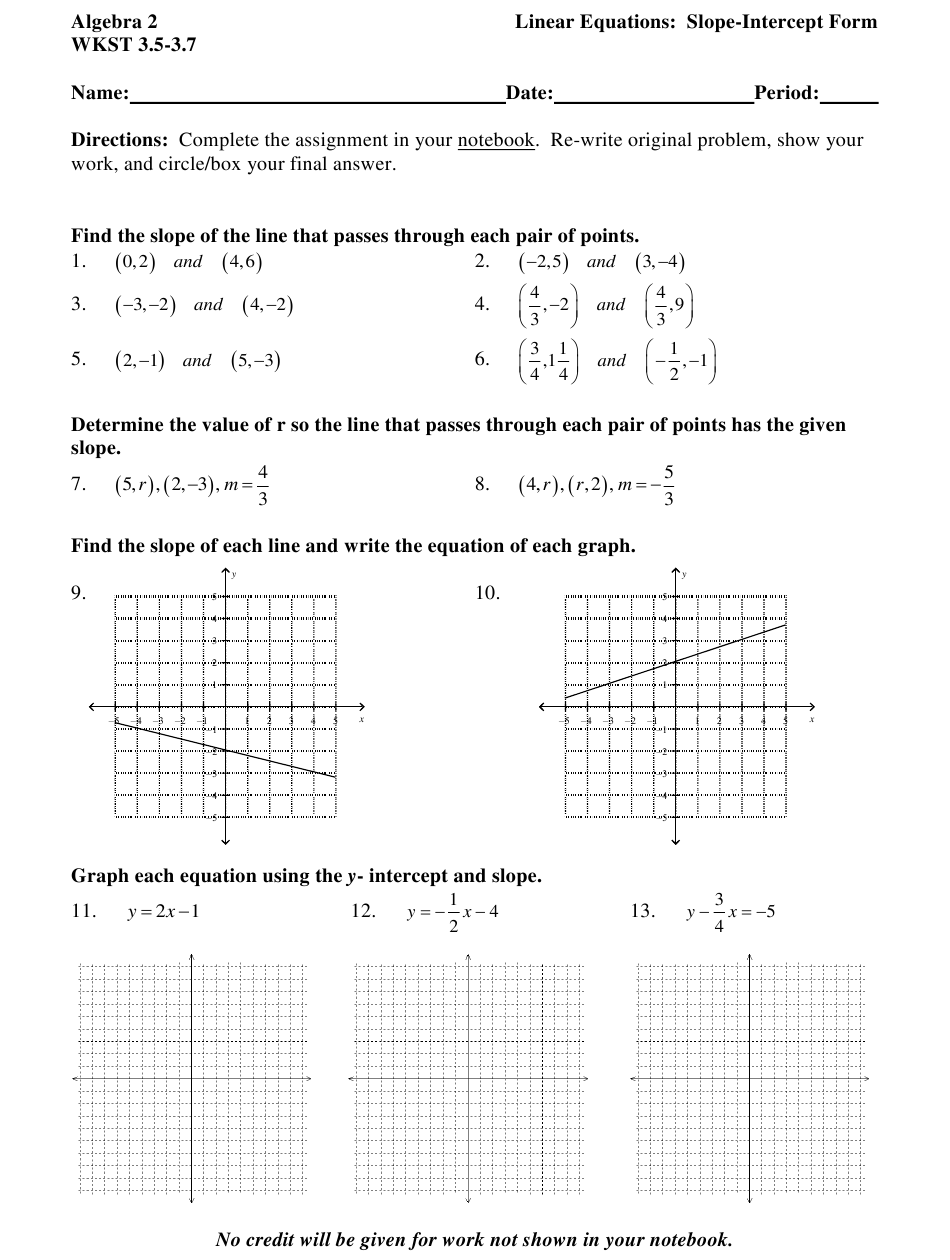
Graph Linear Equations Worksheet: Easy Slope-Intercept Guide

The ability to graph linear equations is an essential skill in mathematics, particularly algebra. Learning how to interpret and plot these equations not only helps in understanding the basics of functions but also in mastering higher-level math concepts. This blog post will guide you through the process of graphing linear equations in the slope-intercept form (y = mx + b) with an easy-to-follow, practical approach.
Understanding Slope-Intercept Form

Before diving into graphing, let's revisit the foundation:
- y: the variable representing the y-coordinate.
- m: the slope of the line, which determines how steep the line is. A positive slope means the line increases as you move from left to right; a negative slope means it decreases.
- b: the y-intercept, where the line crosses the y-axis.
Step-by-Step Guide to Graphing

Identify the Slope and Y-Intercept

From the equation, pick out m (slope) and b (y-intercept). For example, in the equation y = 2x + 3, m is 2 and b is 3.
Plot the Y-Intercept

The y-intercept is your starting point. Plot the point (0, b) on the graph. This point shows where the line touches the y-axis.
Use the Slope to Find Another Point

- Remember, slope (m) is the change in y (Δy) over the change in x (Δx), or rise over run.
- From your y-intercept, move up (or down) for the “rise” and right (or left) for the “run.”
- For example, with m = 2 (which is 2⁄1), move up 2 units and right 1 unit from the y-intercept to find another point on the line.
Draw the Line

Once you have two points, use a straightedge to draw a line through them. This line will extend infinitely in both directions, representing all solutions to the equation.
📝 Note: Ensure to use a straightedge to make your line straight. Any deviation might lead to incorrect interpretations.
Label the Graph

Don’t forget to label your axes, the line, and the scale. This makes your graph informative and useful for others.
Common Mistakes and How to Avoid Them

- Confusing positive and negative slope: Always remember the direction of the line’s ascent or descent.
- Overlooking the y-intercept: The y-intercept is often the most straightforward point to plot; skipping it can lead to misalignment.
- Incorrectly interpreting fractions as slope: When dealing with a slope like 3⁄2, remember the rise is 3, and the run is 2, not vice versa.
Practical Examples

Example 1: y = -1/2x + 4

Here’s how you’d graph this:
- Plot the y-intercept (0, 4).
- Since the slope is -1⁄2, move down 1 unit and right 2 units to find another point.
- Draw the line passing through these points.
| Equation | Points to Plot |
|---|---|
| y = -1/2x + 4 | (0, 4), (2, 3.5) |

Applications of Graphing Linear Equations

- Real-world Scenarios: Understanding slope and intercept helps predict outcomes like profit, distance covered, or the performance of systems.
- Problem Solving: Graphing aids in solving systems of equations by showing where lines intersect.
- Visual Learning: For many, seeing the graph helps in understanding the behavior of the equation visually.
As we reach the end of this journey through the linear equation landscape, remember that graphing is not just about plotting points but about visualizing relationships, trends, and potential outcomes. It's a tool that turns abstract numbers into something tangible and often intuitive. By mastering this skill, you unlock the ability to interpret data, solve problems more efficiently, and predict the future with greater accuracy. Whether you're analyzing stock trends, planning a budget, or simply trying to understand the progression of time and distance, graphing linear equations in slope-intercept form is a fundamental skill that transcends the classroom.
Why is it important to use a straightedge when graphing?

+
Using a straightedge ensures that the line you draw is straight, which is crucial for accurately representing the linear equation and avoiding misinterpretation.
Can I graph an equation with a zero slope?

+
Yes, a line with a zero slope (y = b) is a horizontal line. You would plot the y-intercept, and the line would extend infinitely left and right parallel to the x-axis.
What does a slope of undefined mean in graphing?
+
An undefined slope means the line is vertical, running along the y-axis with no horizontal movement. The equation would look like x = c, where c is a constant.