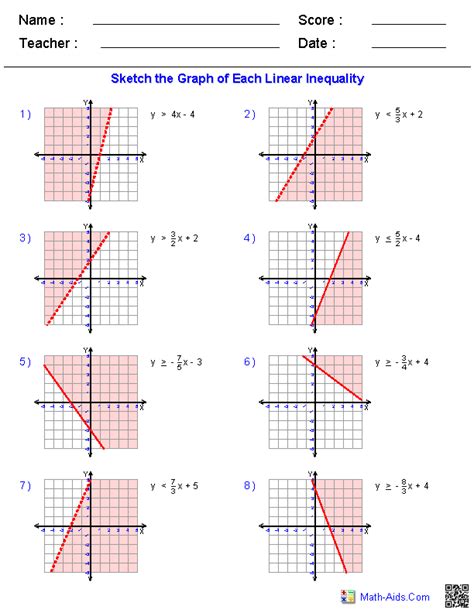
Graphing Inequalities Worksheet with Answers and Examples
Understanding Graphing Inequalities

Graphing inequalities is a fundamental concept in mathematics, particularly in algebra and geometry. It involves representing solutions to inequalities on a coordinate plane. Inequalities can be expressed in various forms, including linear and quadratic inequalities.
What are Inequalities?

Inequalities are mathematical statements that compare two expressions using inequality symbols such as less than (<), greater than (>), less than or equal to (≤), and greater than or equal to (≥). For example:
- 2x + 3 > 5
- x - 2 ≤ 3
- x^2 + 4x - 5 ≥ 0
How to Graph Inequalities

To graph an inequality, follow these steps:
- Write the inequality in slope-intercept form: Rewrite the inequality in the form y = mx + b, where m is the slope and b is the y-intercept.
- Graph the related equation: Graph the equation obtained by replacing the inequality symbol with an equal sign (=).
- Shade the region: Shade the region above or below the line, depending on the inequality symbol.
Example 1: Graphing a Linear Inequality
Graph the inequality 2x + 3 > 5.
- Write the inequality in slope-intercept form: y > -2x + 2
- Graph the related equation: y = -2x + 2
- Shade the region: Shade the region above the line.
📝 Note: When graphing a greater than (>), shade the region above the line. When graphing a less than (<), shade the region below the line.
Example 2: Graphing a Quadratic Inequality
Graph the inequality x^2 + 4x - 5 ≥ 0.
- Write the inequality in factored form: (x + 5)(x - 1) ≥ 0
- Graph the related equation: (x + 5)(x - 1) = 0
- Shade the region: Shade the region where the expression (x + 5)(x - 1) is non-negative.
| Inequality Symbol | Shading Region |
|---|---|
| > (greater than) | Above the line |
| < (less than) | Below the line |
| ≥ (greater than or equal to) | Above and on the line |
| ≤ (less than or equal to) | Below and on the line |

Worksheets with Answers and Examples

Here are some examples of graphing inequalities worksheets with answers:
Worksheet 1: Linear Inequalities
- Graph the inequality x - 2 > 3. Answer: Shade the region above the line y = x - 2 + 3.
- Graph the inequality 2x + 1 ≤ 5. Answer: Shade the region below the line y = -2x + 1 - 5.
Worksheet 2: Quadratic Inequalities
- Graph the inequality x^2 - 4x - 3 ≥ 0. Answer: Shade the region where the expression (x - 3)(x + 1) is non-negative.
- Graph the inequality x^2 + 2x - 6 < 0. Answer: Shade the region where the expression (x + 3)(x - 2) is negative.
Conclusion

Graphing inequalities is an essential skill in mathematics, and it requires attention to detail and a clear understanding of the inequality symbols. By following the steps outlined in this article and practicing with worksheets, you can become proficient in graphing inequalities and develop a deeper understanding of mathematical concepts.
What is the difference between a linear and quadratic inequality?

+
A linear inequality has a degree of 1, whereas a quadratic inequality has a degree of 2.
How do I determine which region to shade when graphing an inequality?

+
Use the inequality symbol to determine the shading region. For example, if the symbol is >, shade the region above the line.
Can I graph an inequality with a fractional coefficient?

+
Yes, you can graph an inequality with a fractional coefficient. Simply rewrite the inequality in slope-intercept form and proceed with graphing.
Related Terms:
- Graphing inequalities worksheet pdf
- Graphing Linear Inequalities Worksheet
- Graphing inequalities worksheet answer key