5 Tips for Graphing Slope Intercept Form Easily

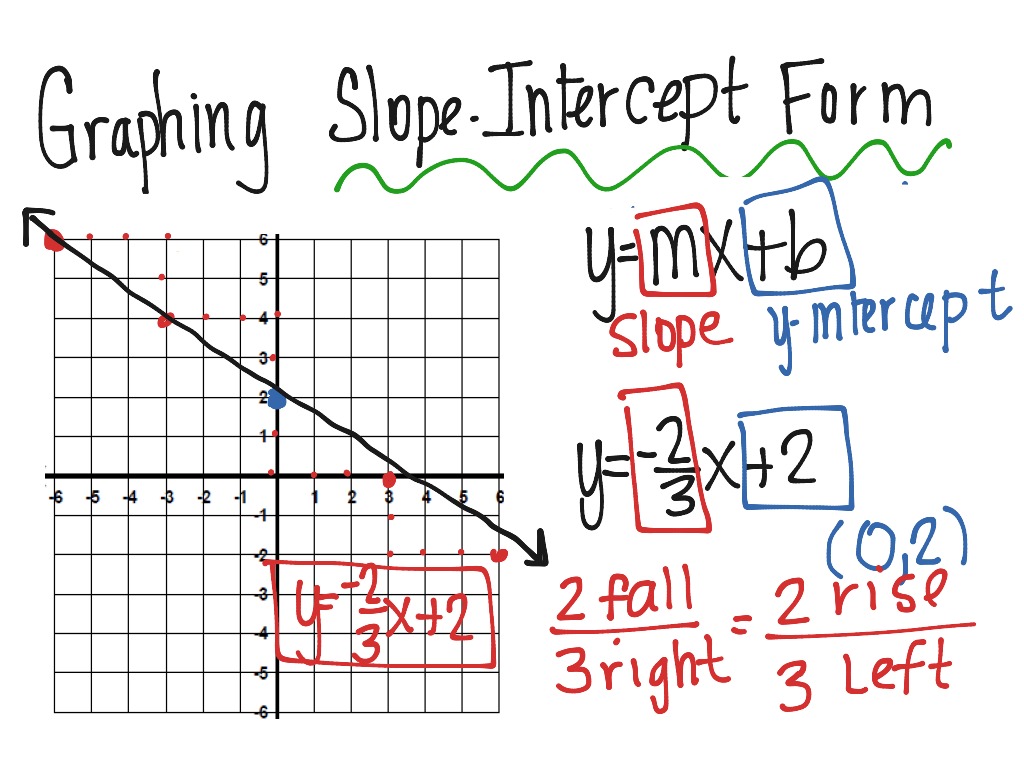
Understanding and graphing equations in slope intercept form, y = mx + b, is a fundamental skill in algebra. This form provides a direct path to interpreting the steepness (slope) and the point where the line crosses the y-axis (y-intercept). Here, we'll explore five actionable tips that make graphing these equations not only easier but also more precise.
Tip 1: Utilize Graph Paper

- Precision is Key: Graph paper allows for precise plotting of points. The grid makes it easier to count intervals accurately.
- Create a Guide: Draw a vertical and horizontal line through the origin to help keep your plot organized.
How to Use Graph Paper:

- Identify the y-intercept b from your equation.
- Plot this point directly on the y-axis.
- Use the slope m to find the next point: for each unit right or left on the x-axis, move m units up or down on the y-axis.
- Draw a line through these points.
Tip 2: Plot Multiple Points for Accuracy

Graphing a line from just two points can be misleading due to potential mistakes in calculations or graph reading.
- Calculate several points from the equation to confirm the line's direction.
- Plot these points, then use a straight edge to draw your line through them, enhancing accuracy.
📏 Note: Evenly spaced points along the line provide a robust check for correct plotting.
Tip 3: Make Use of Slope Characteristics
| Slope Sign | Line Direction |
|---|---|
| Positive m | Up from Left to Right |
| Negative m | Down from Left to Right |
| m = 0 | Horizontal Line |
| Undefined | Vertical Line |

By understanding these characteristics, you can:
- Know in which quadrant the line should be drawn before plotting.
- Get an immediate idea of the line's behavior, aiding in faster, confident plotting.
Tip 4: Consider the y-intercept

Here are steps to effectively use the y-intercept:
- Locate b: Directly find where your line will touch the y-axis.
- Plot the y-intercept: This point is already known, reducing calculation errors.
- Use b as your starting point: It's a reliable reference when you find and plot other points using the slope.
Tip 5: Practice Graphing Slope Intercept Forms

Consistent practice sharpens your skillset, making each subsequent graph quicker and more accurate:
- Create Visual Aids: Draw diagrams or use apps for interactive practice. This reinforces visual understanding.
- Vary Equations: Practice with different values for m and b, including fractions and negative numbers, to challenge yourself.
- Understand Real-World Applications: Recognize that this form is used in finance, economics, physics, and many other fields for modeling scenarios.
In summary, mastering the art of graphing in slope intercept form involves careful attention to precision, understanding the inherent properties of the slope and y-intercept, and practicing regularly to improve speed and accuracy. With these five tips, you can approach any problem involving linear equations with confidence, knowing exactly how to interpret, plot, and verify your work.
What is Slope Intercept Form?

+
Slope intercept form is an equation of a line written as y = mx + b, where m is the slope of the line and b is the y-intercept, the point where the line crosses the y-axis.
Can I graph a line with only the slope?

+
While knowing the slope is crucial, you also need a point to start from. Typically, the y-intercept gives you this point directly.
What if the slope is a fraction?

+
Graphing with a fractional slope means counting units in a different way. For example, if the slope is 1⁄2, for every 1 unit to the right on the x-axis, move up half a unit on the y-axis.