Cube Root Functions: Graphing Worksheet for Students
Understanding cube root functions is not only fascinating but also crucial for students delving into the realms of algebra and geometry. Cube roots, being inverses to the cube function, offer a unique perspective on how numbers interact, shaping the graph into distinct patterns. Today, we'll explore how to graph cube root functions, providing students with a structured approach to visualize these complex entities.
Understanding Cube Roots

The cube root of a number ( x ) is another number ( y ) such that ( y^3 = x ). The function for a cube root can be represented as ( f(x) = \sqrt[3]{x} ). Here are a few key points to understand before we delve into graphing:
- The cube root of zero is zero.
- For positive values of ( x ), the cube root function yields positive results.
- For negative values of ( x ), the cube root function yields negative results.
- The cube root function passes through the origin (0,0).
The Basic Cube Root Function: ( f(x) = \sqrt[3]{x} )


Let's start with the simplest form of the cube root function.
- The graph will always cross the x-axis at x = 0 since 0 = 0 .
- It extends to both positive and negative infinity, smoothly curving outward from the origin in both directions.
- The function has no asymptotes as it is continuous for all real numbers.
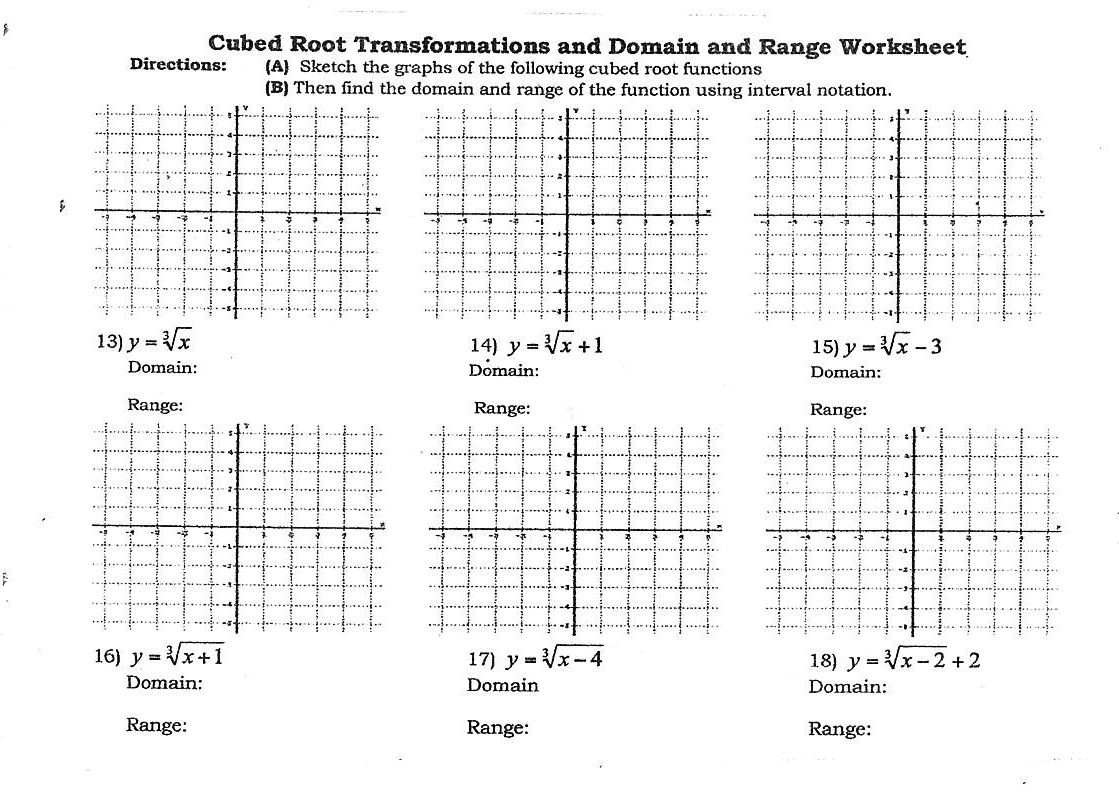
To graph this, follow these steps:
- Plot the point (0,0).
- Plot some key points: (1,1), (-1,-1), (8,2), (-8,-2), (27,3), (-27,-3), etc.
- Connect these points with a smooth curve that reflects the shape of a cube root.
⚠️ Note: Always ensure your graph extends to both positive and negative directions to reflect the function's behavior.
Transformations of Cube Root Functions
Cube root functions can be transformed to fit different shapes and positions on the graph. Here are the common transformations:
Vertical Stretch or Compression
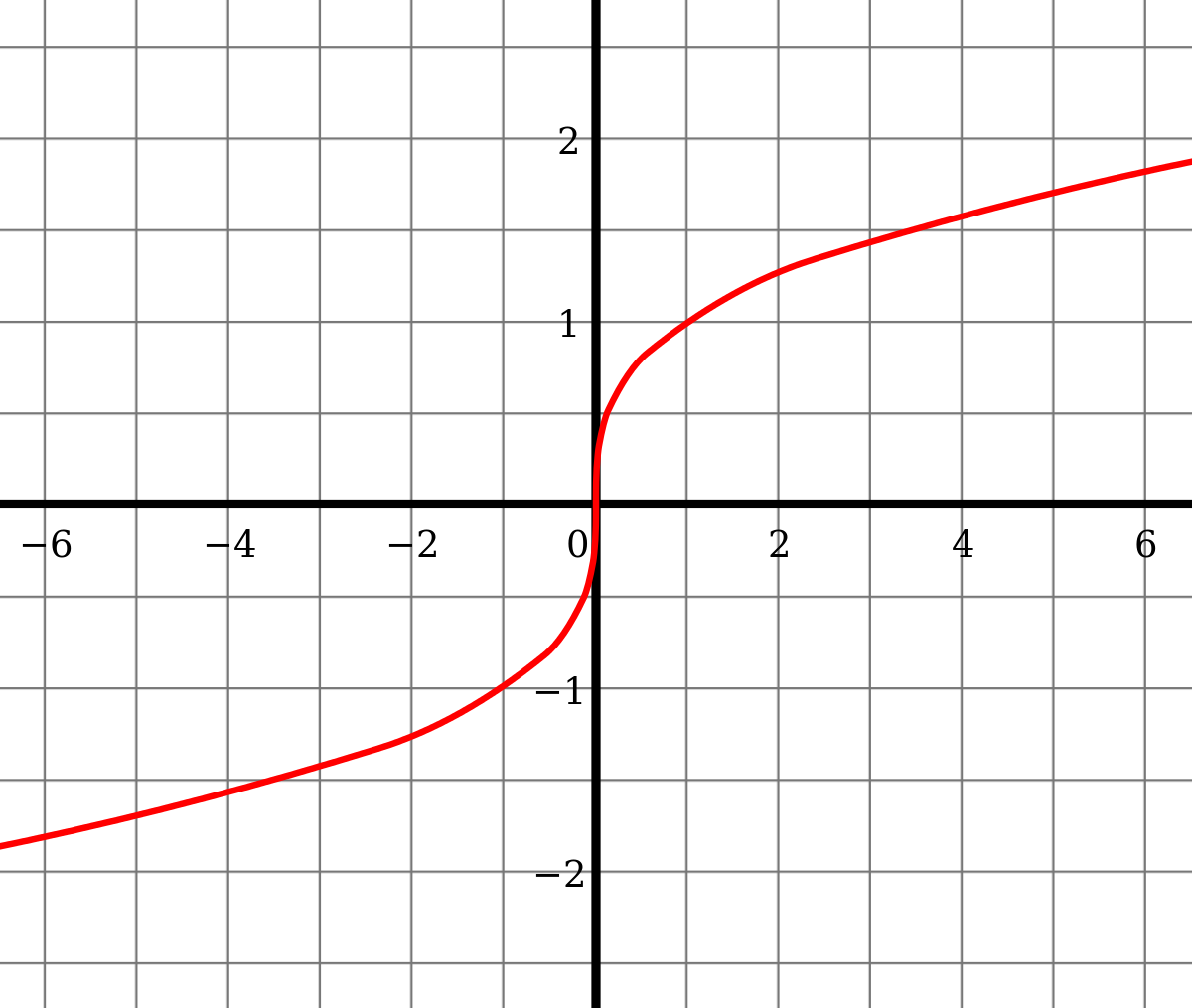
The function ( f(x) = a\sqrt[3]{x} ), where ( a ) is a non-zero constant, stretches or compresses the graph vertically. If ( |a| > 1 ), the graph stretches, and if ( |a| < 1 ), it compresses.
Horizontal Stretch or Compression

Given by ( f(x) = \sqrt[3]{a x} ), where ( a \neq 0 ), this transformation affects the x-axis. A larger ( |a| ) compresses the graph horizontally, and a smaller ( |a| ) stretches it.
Vertical Shift

Adding or subtracting a constant ( b ) to the function results in a vertical shift: ( f(x) = \sqrt[3]{x} + b ). Adding ( b ) shifts the graph up, and subtracting shifts it down.
Horizontal Shift

To move the graph left or right, we modify the x-coordinate: ( f(x) = \sqrt[3]{x - h} ). If ( h > 0 ), the graph shifts right, and if ( h < 0 ), it shifts left.
To graph these transformations, one must:
- Determine the base transformation by calculating the change in shape or position.
- Adjust points from the basic graph accordingly.
- Sketch the new curve with the transformed points.
Application: Real-Life Example
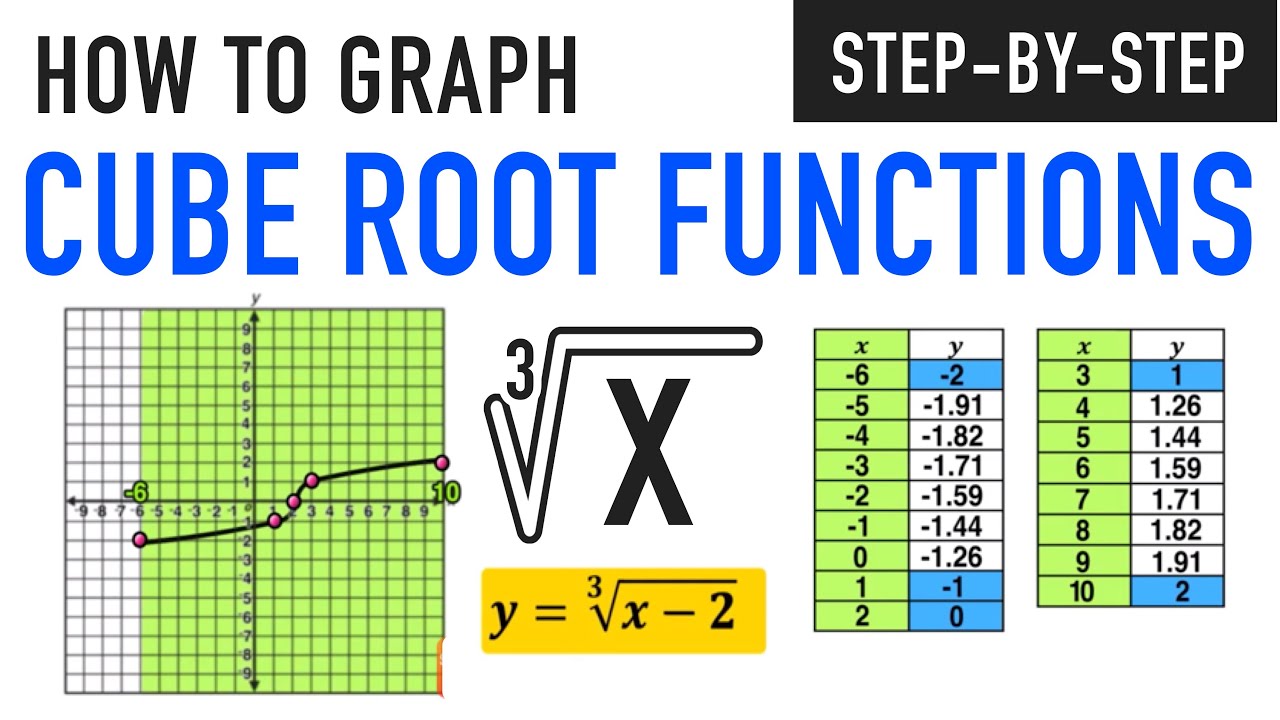
Imagine you're a civil engineer calculating the depth of a water tank where the volume is directly proportional to the cube of the depth. You can use a cube root function to find how deep the water must be for a certain volume:
| Volume (V in cubic meters) | Depth (d in meters) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 8 | 2 |
| 27 | 3 |

This example can be modeled by the function d = \sqrt[3]{V} , where d is the depth and V is the volume. Plotting this on a graph would help visualize the relationship.
Putting it into Practice
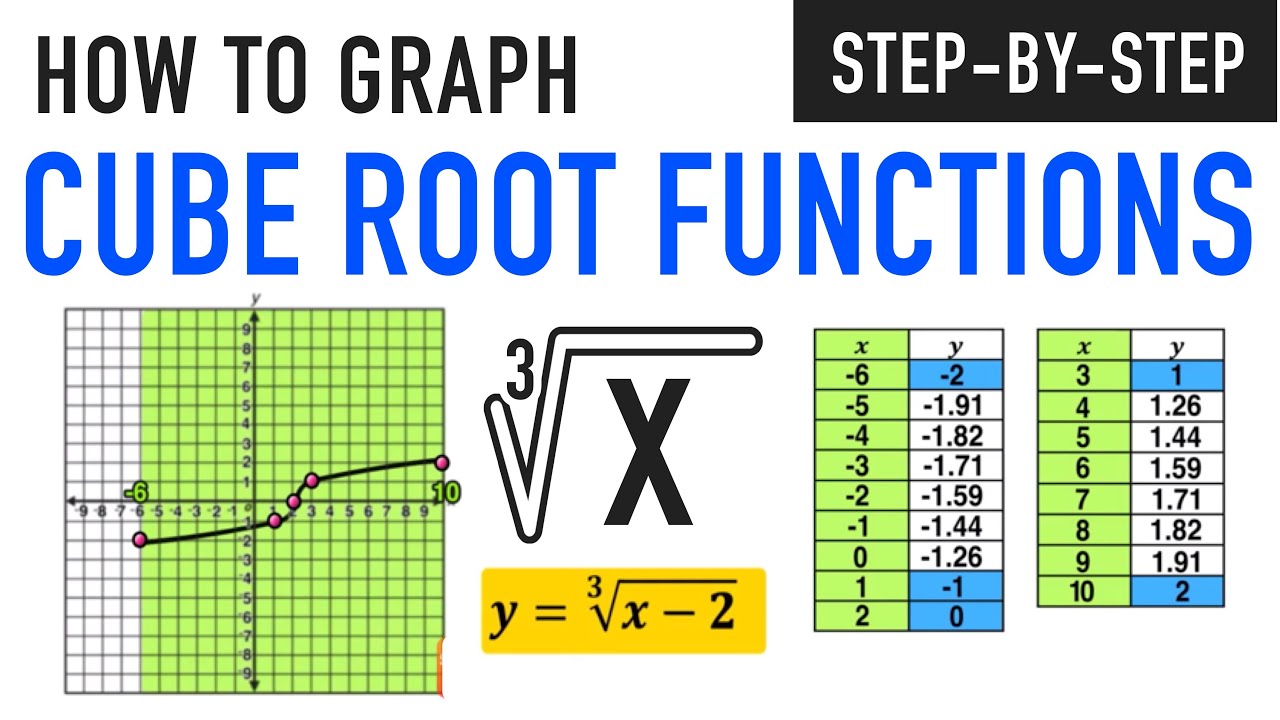
Here’s a small worksheet for students to practice:
Exercise:
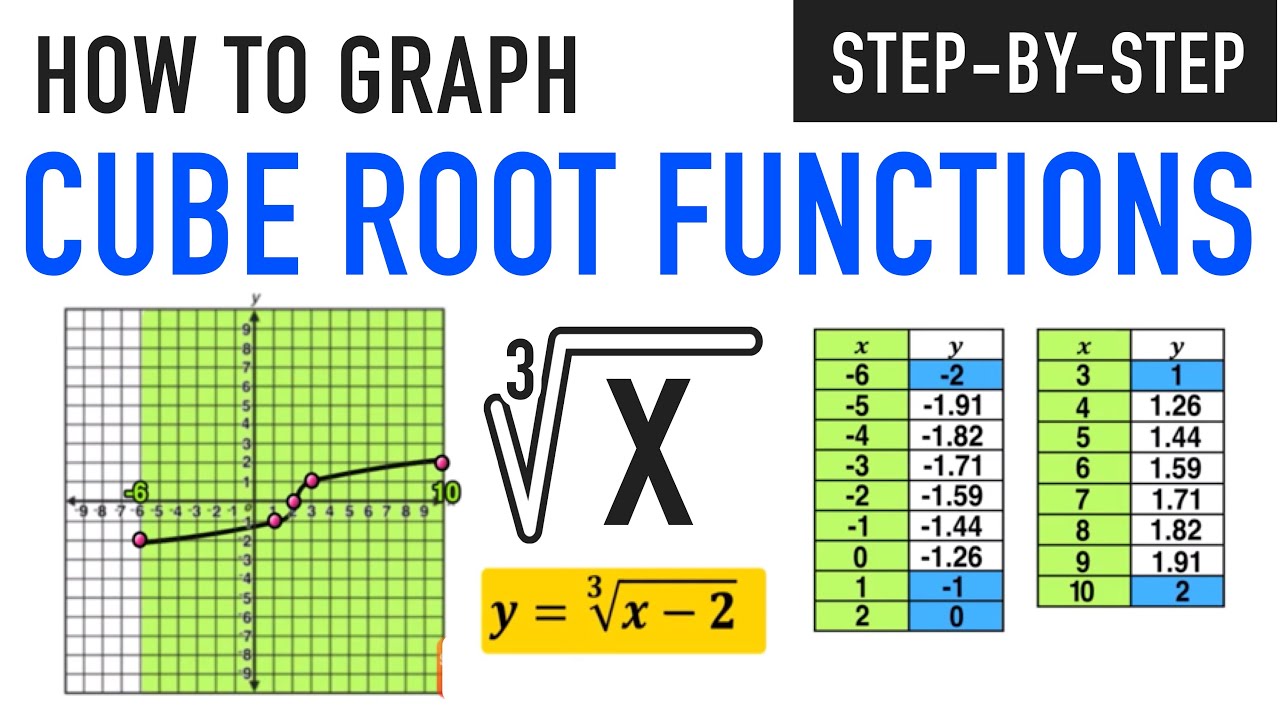
- Graph the function ( f(x) = \sqrt[3]{x} - 2 ).
- Explain how the graph of ( f(x) = \sqrt[3]{x} ) changes when transformed into ( f(x) = \sqrt[3]{x} + 3 ).
👁️ Note: When plotting, consider the domain and range of each transformed function carefully.
Graphing cube root functions provides a profound insight into how algebraic functions can translate into visual representations. Understanding these transformations not only sharpens mathematical skills but also encourages a deeper appreciation for how functions behave in different scenarios. Whether in real-life applications or pure mathematical exploration, the ability to graph and interpret cube root functions is an invaluable skill.
How do I know if the cube root function will cross the y-axis?

+
The cube root function ( f(x) = \sqrt[3]{x} ) will always cross the y-axis at y = 0. However, if the function is shifted vertically (e.g., ( f(x) = \sqrt[3]{x} + b )), it will cross the y-axis at y = b.
Can cube root functions have a vertical asymptote?

+
No, cube root functions do not have vertical asymptotes because they are continuous over the entire real number line. They smoothly curve through all points, without gaps or breaks.
Why is it important to graph cube root functions?

+
Graphing cube root functions helps students visualize abstract algebraic concepts, understand how these functions behave under various transformations, and apply this knowledge to real-world problems or further mathematical studies.



