Master Absolute Value Graphing with Our Fun Worksheet

Delving into the world of mathematics, one of the core concepts that can both simplify and enhance your understanding of functions and their behaviors is graphing the absolute value. Here's a comprehensive guide on mastering absolute value graphing, complete with a fun worksheet to practice your skills, ensuring that you not only learn but also enjoy the process.
What is Absolute Value?

Absolute value is a mathematical operation that transforms a number to its distance from zero on the number line, disregarding the sign. Essentially, the absolute value of any number is always non-negative. If you have a number x, its absolute value, denoted as |x|, is defined as:
- |x| = x if x ≥ 0
- |x| = -x if x < 0
This operation is crucial in algebra, particularly in solving equations, inequalities, and in plotting graphs.
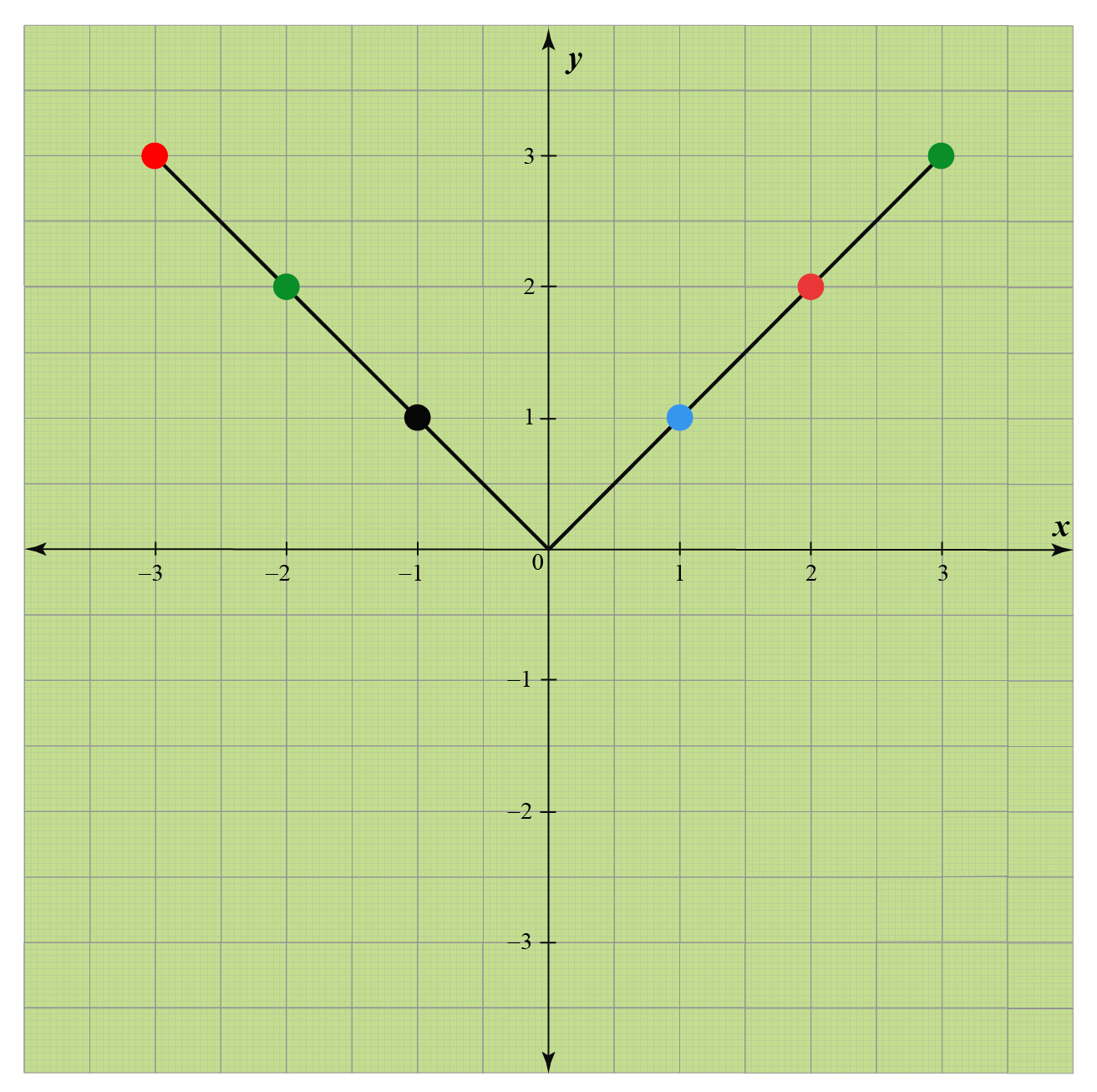
Understanding the Absolute Value Graph
The graph of y = |x| is a V-shaped curve that opens upward. Here’s how to construct this graph:
- At x = 0, the graph touches the y-axis at y = 0.
- For all values of x greater than 0, y = x.
- For all values of x less than 0, y = -x, which reflects the positive values over the y-axis.
Now, let's delve deeper into transforming this basic graph for different equations.
Transformations of Absolute Value Graphs
Vertical and Horizontal Shifts

Shifting the graph vertically or horizontally alters its position on the coordinate plane:
- Vertical Shift: If y = |x| + k, the graph shifts up by k units. If k is negative, it shifts down.
- Horizontal Shift: For y = |x - h|, the graph shifts h units to the right. If h is negative, it shifts to the left.
Reflections
Reflecting the graph changes its direction:
- Reflection over the x-axis: y = -|x| flips the graph so it opens downward.
- Reflection over the y-axis: This transformation involves a change in the form of the equation, where x is replaced by -x.
Stretching and Compressing

The graph can be vertically stretched or compressed:
- Vertical Stretch: y = a|x| where a > 1 makes the graph narrower, and 0 < a < 1 makes it wider.
- Vertical Compression: If a is a fraction less than 1, the graph gets stretched horizontally.
Combining Transformations
Multiple transformations can be applied simultaneously, for example, in y = -2|x - 3| + 5, which involves:
- Horizontal shift right by 3 units
- Vertical stretch by a factor of 2
- Reflection over the x-axis
- Vertical shift up by 5 units
Mastering with a Worksheet
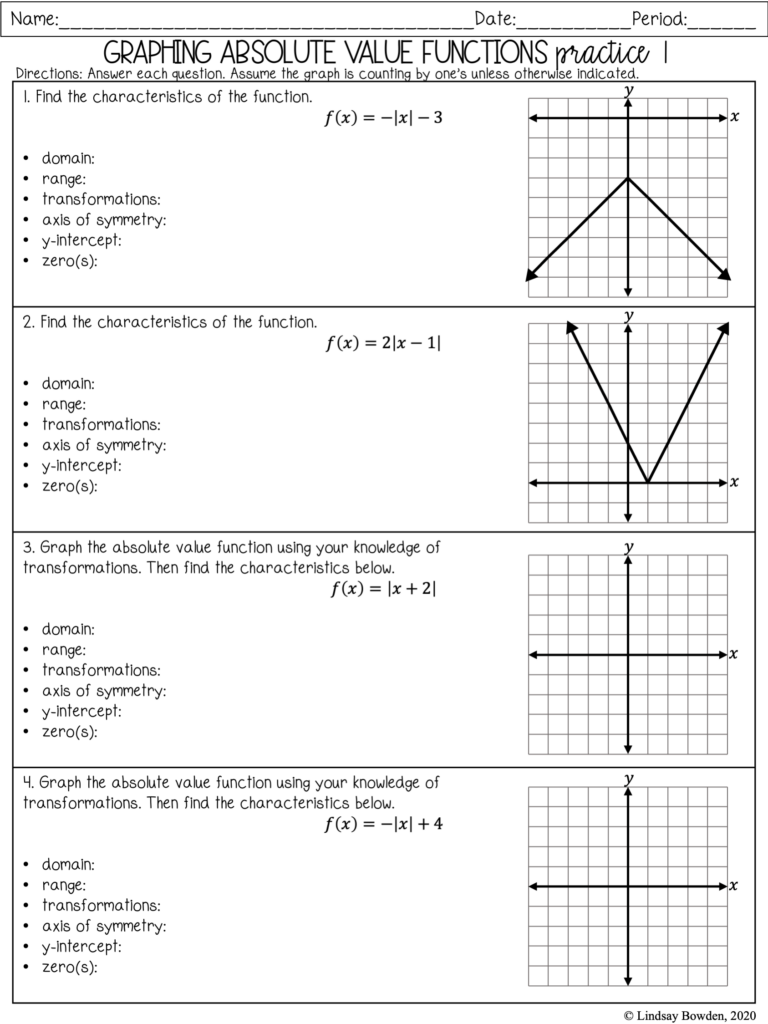
To truly grasp these concepts, applying them in practice is essential. Here’s a worksheet for graphing absolute value functions:
| Equation | Graph Shape | Features to Note |
|---|---|---|
| y = |x| | V shape, opens up | Vertex at (0,0) |
| y = |x + 4| | V shape, opens up, shifted left | Vertex at (-4,0) |
| y = 2|x| - 3 | V shape, narrower, shifted down | Vertex at (0,-3) |
| y = -|x - 2| + 1 | V shape, opens down, shifted right | Vertex at (2,1) |

📝 Note: When graphing, always identify the vertex first, then plot several points on either side to outline the shape.
Practical Applications

Understanding absolute value graphs is not just for academic purposes. Here are some practical applications:
- Electronics and Signals: Absolute values are used to represent signal strengths in electronics without considering direction.
- Distances: In real-life problems involving distances, absolute values ensure the calculation of the actual distance, regardless of direction.
- Error Analysis: In statistical models or error correction, absolute values give the magnitude of the error.
The beauty of mastering absolute value graphing is not only in the ability to solve complex equations but also in the patterns and symmetry that emerge, making the concept both practical and aesthetically pleasing. This worksheet serves as a stepping stone towards a deeper understanding of not just absolute value but also of transformations in mathematics. As you work through these exercises, remember that each new equation you encounter offers a chance to visualize and manipulate mathematical concepts in new and exciting ways. Embrace the challenge, and you'll find that your ability to navigate the landscape of mathematics will be significantly enhanced.
What does the vertex of an absolute value graph represent?

+
The vertex of an absolute value graph signifies the point where the graph changes direction. For a basic absolute value function like y = |x|, this point is at (0,0), indicating the lowest point of the V-shape. When transformations are applied, this point moves, reflecting the shift, stretch, or compression of the graph.
Why do we need absolute value graphs?

+
Absolute value graphs are crucial for understanding and solving problems involving distance, error analysis, and in fields like electronics and statistics where direction is less important than the magnitude of a value. They also help in visualizing the concept of functions and their behavior under transformations.
Can absolute value graphs have negative y-values?

+
Yes, absolute value graphs can have negative y-values. For example, if the graph is reflected over the x-axis, it will open downward, allowing for y-values less than zero. However, the absolute value itself always remains non-negative.
How do I identify transformations in an absolute value equation?

+
Look for:
- Addition or subtraction inside the absolute value for horizontal shifts.
- Addition or subtraction outside for vertical shifts.
- Multiplication or division outside for vertical stretch or compression.
- A negative sign outside for reflection over the x-axis.
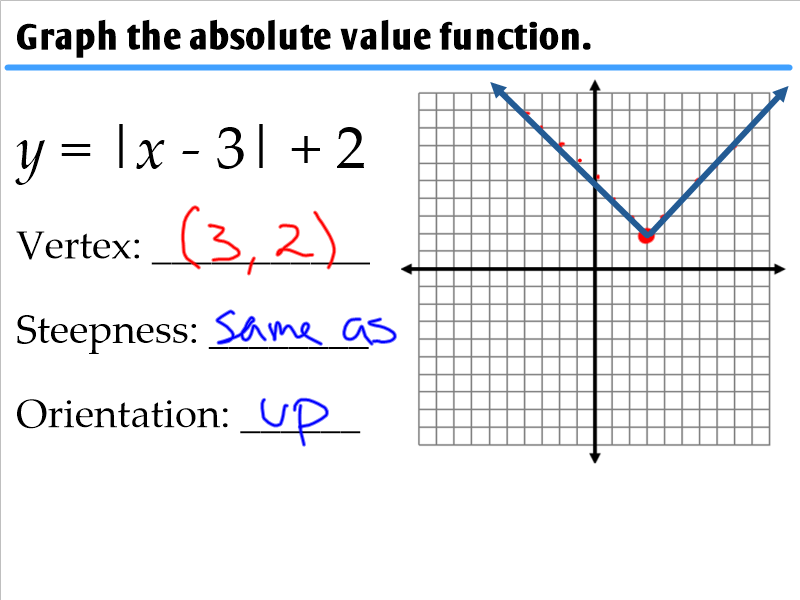
How can I use the worksheet to improve my graphing skills?
+
The worksheet provides a structured approach to practice:
- Work through each equation step-by-step, plotting key points like the vertex.
- Use different colors to distinguish between different transformations.
- Check your answers by graphing on graphing software or calculator for comparison.