Master Absolute Value Graphs: Beginner-Friendly Worksheet

Do you remember staring blankly at the graph of an absolute value function during your high school algebra class, wondering why it looked like the iconic "V" shape? It's time to demystify the absolute value graph with this beginner-friendly worksheet. Absolute value functions can seem daunting at first, but with a bit of understanding and practice, you'll find their graphs both fun and intuitive.
What is an Absolute Value Function?
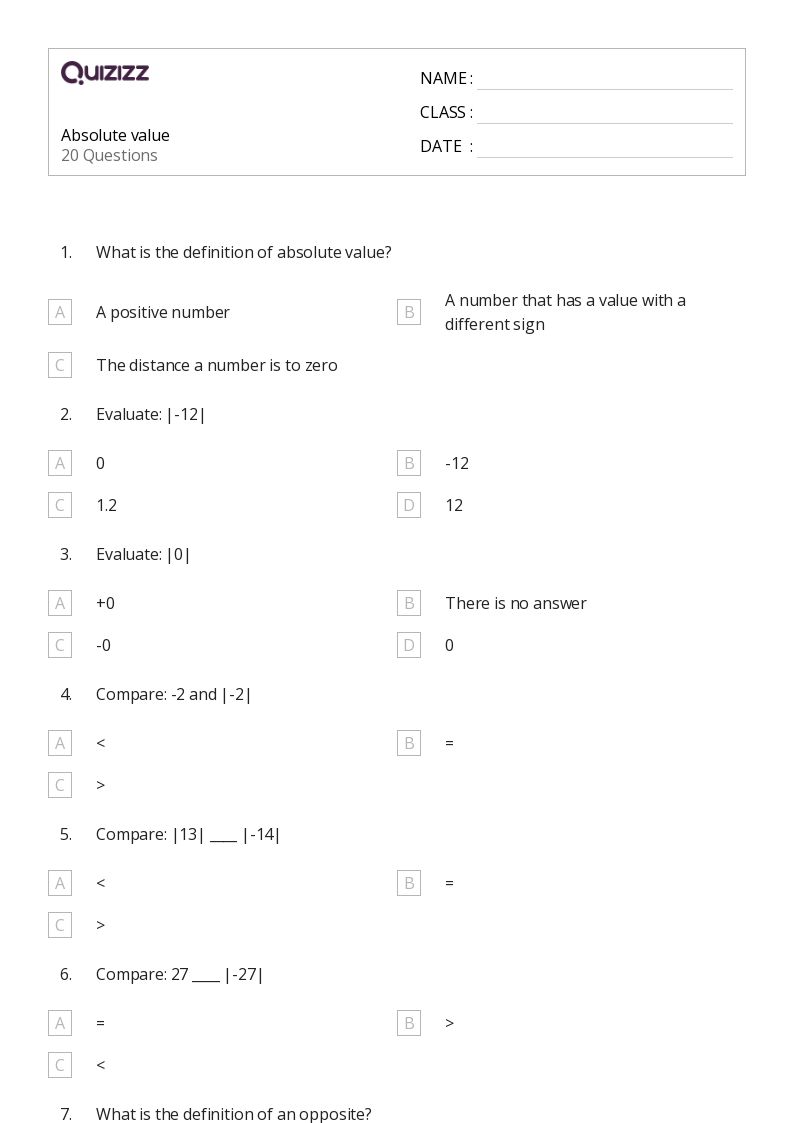
At its core, an absolute value function transforms any number into its positive equivalent. For instance, |3| and |-3| both equal 3. In mathematics, this is expressed as f(x) = |x|, where f(x) is the output or function value for a given input x.

Graphing Absolute Value Functions

Let’s delve into how we construct the graph of an absolute value function.
The Basic Structure

- The standard form of an absolute value function is f(x) = |x|. Its graph is a “V” shape.
- The vertex of this V is at the point (0, 0), which means the function has a minimum value of 0 at x = 0.
Shifting the Graph
We can shift this graph both vertically and horizontally:
- Vertical Shifts: f(x) = |x| + b shifts the graph up (b > 0) or down (b < 0) by b units.
- Horizontal Shifts: f(x) = |x - h| moves the graph left (h > 0) or right (h < 0) by h units.
Reflections and Stretching

Let’s explore reflections and stretching:
- Reflecting over the x-axis: f(x) = -|x| flips the “V” upside down, creating an “upside-down V.”
- Stretching or compressing: f(x) = a|x|, where |a| > 1 stretches the graph, making it thinner, while 0 < |a| < 1 compresses it, making it wider.
Steps to Graph Absolute Value Functions

Follow these steps to graph any absolute value function:
- Identify the basic function: Start with the graph of f(x) = |x|.
- Shifts: Determine the values of h and b from f(x) = |x - h| + b to shift the graph.
- Reflection: If there’s a negative sign outside, reflect the graph over the x-axis.
- Scaling: If there’s a coefficient a, stretch or compress the graph accordingly.
- Plot Key Points: Plot points like the vertex, where the graph intersects the axes, or any other significant points you can calculate.
- Sketch the Graph: Connect these points smoothly to form the characteristic “V” shape or its variations.
📝 Note: Remember that each point on the graph of an absolute value function should always be above or on the x-axis because absolute values are non-negative.
Examples of Absolute Value Graphs

Let’s look at some examples to solidify our understanding:
Example 1: Basic Absolute Value Function

Consider f(x) = |x|:
- The graph is a simple “V” with its vertex at (0, 0).
- It’s symmetrical about the y-axis.
Example 2: Horizontal Shift

Consider f(x) = |x - 2|:
- Move the graph to the right by 2 units. The vertex now is at (2, 0).
Example 3: Vertical Shift and Reflection

Consider f(x) = -|x| + 3:
- Reflect the graph over the x-axis, turning the “V” upside down.
- Then shift it up by 3 units. The new vertex is at (0, 3).
Common Mistakes in Graphing Absolute Value Functions

Here are a few common pitfalls:
- Ignoring Symmetry: The graph is symmetrical; what happens on one side of the y-axis must happen on the other side as well.
- Misplacing the Vertex: The vertex might shift or reflect, but it’s always at the lowest or highest point of the V-shape.
- Confusing Stretching/Compression: Be careful with scaling factors; they can change the steepness of the “V” shape.
Why Absolute Value Graphs Matter
Absolute value functions are not just theoretical exercises; they model real-world phenomena:
- In physics, they represent potential energy graphs where the minimum energy point corresponds to the vertex.
- In optimization problems, they’re used to model cost functions where the absolute minimum cost is sought.
- In finance, they can represent distances from a target value, like in the context of stock price movement.
Conclusion
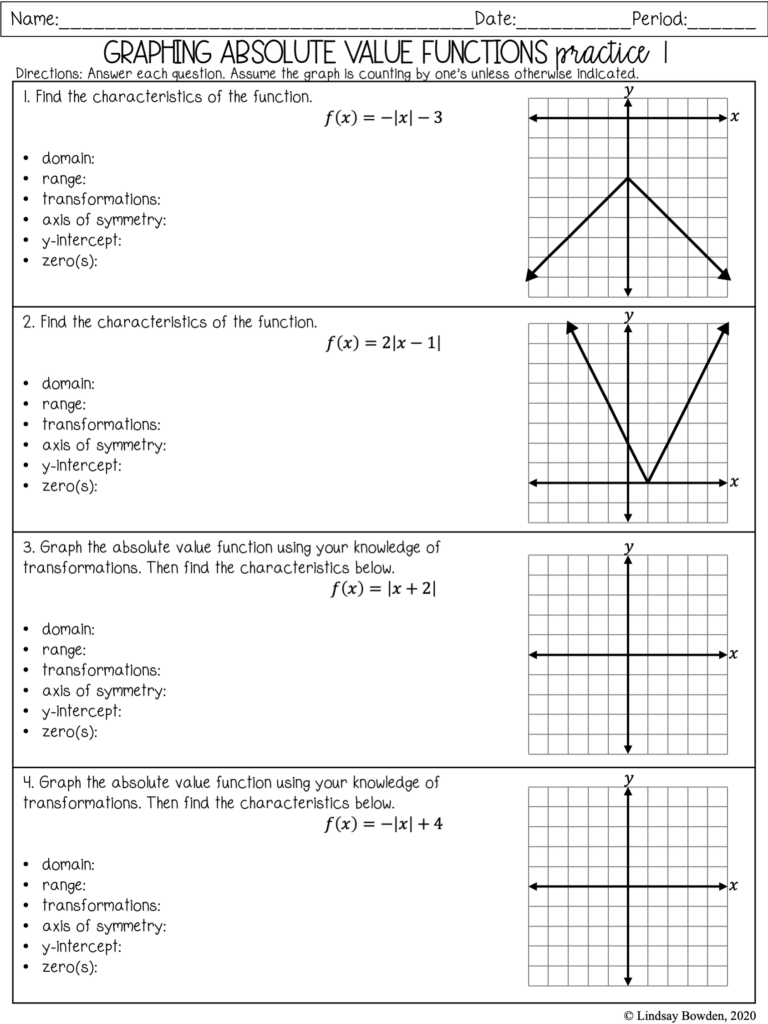
Graphing absolute value functions, initially seeming complex, provides a fantastic opportunity to understand symmetry, transformations, and real-world applications in mathematics. By breaking down each part of the function, from basic shapes to shifts and transformations, you can confidently graph any absolute value function. This skill not only helps with algebra homework but also equips you with the visual and analytical tools to tackle more complex mathematical functions and problems in your academic and practical life.
What makes absolute value functions unique?

+
Their “V” shape and the non-negative values they yield set them apart. Also, the symmetry about the y-axis is a defining characteristic.
Can an absolute value graph be below the x-axis?

+
No, because absolute value functions always return positive values, their graphs will be on or above the x-axis.
How do vertical and horizontal shifts affect the vertex of an absolute value function?

+
Vertical shifts move the vertex up or down along the y-axis, while horizontal shifts move the vertex left or right along the x-axis.