5 Simple Steps to Graph Sine and Cosine Functions

Understanding sine and cosine functions is fundamental for anyone delving into the world of trigonometry, physics, and various engineering disciplines. These functions are not only essential for calculations involving angles but are also integral in modeling periodic phenomena like waves and oscillations. Here, we'll guide you through 5 simple steps to graph sine and cosine functions effectively, ensuring you grasp their behavior, characteristics, and practical applications.
Understanding the Unit Circle
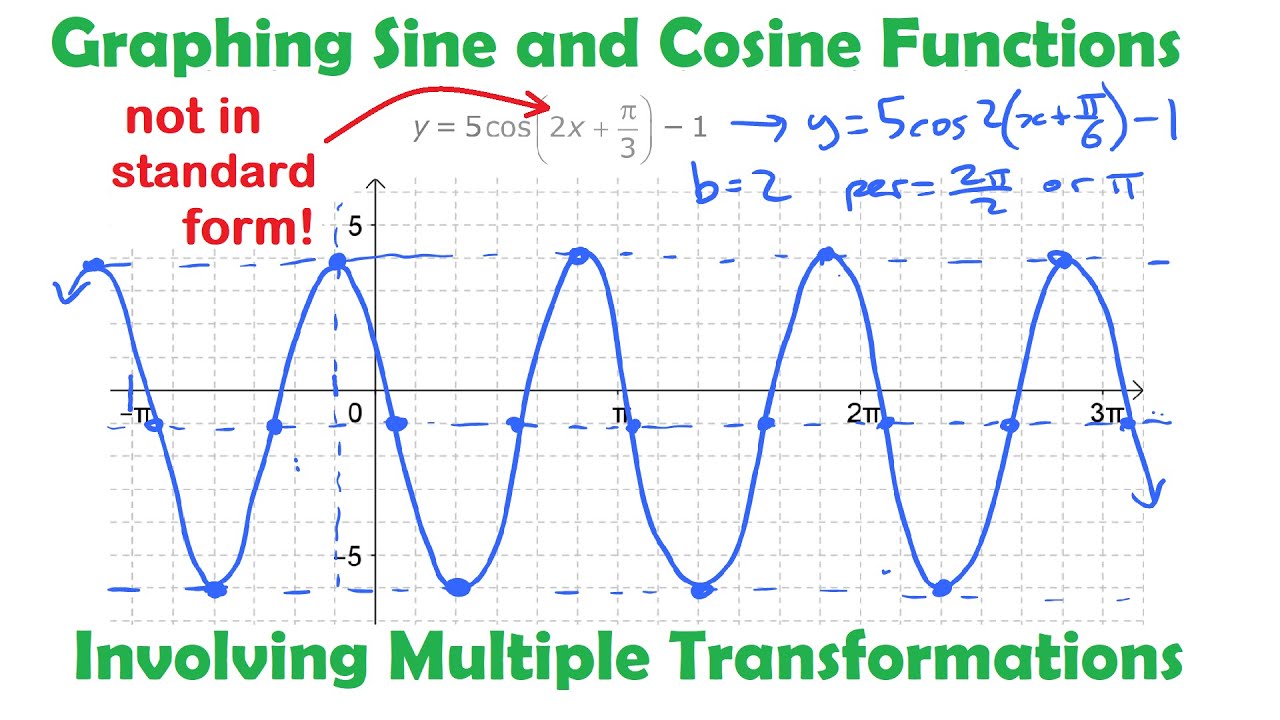
Before graphing, let’s briefly discuss the unit circle, which is the foundation of sine and cosine functions. The unit circle is a circle with a radius of one unit, centered at the origin of a coordinate system.
- The sine of an angle in the unit circle is the y-coordinate of the corresponding point on the circle.
- The cosine of an angle is the x-coordinate of that same point.
Step 1: Setting the Axis

Start by setting up your coordinate system:
- Draw a horizontal x-axis, representing the angle or time variable (usually labeled as θ or t).
- Draw a vertical y-axis, representing the amplitude or function value.
Choose scales that will fit several periods of your sine and cosine waves, with adequate space for labels and ticks.
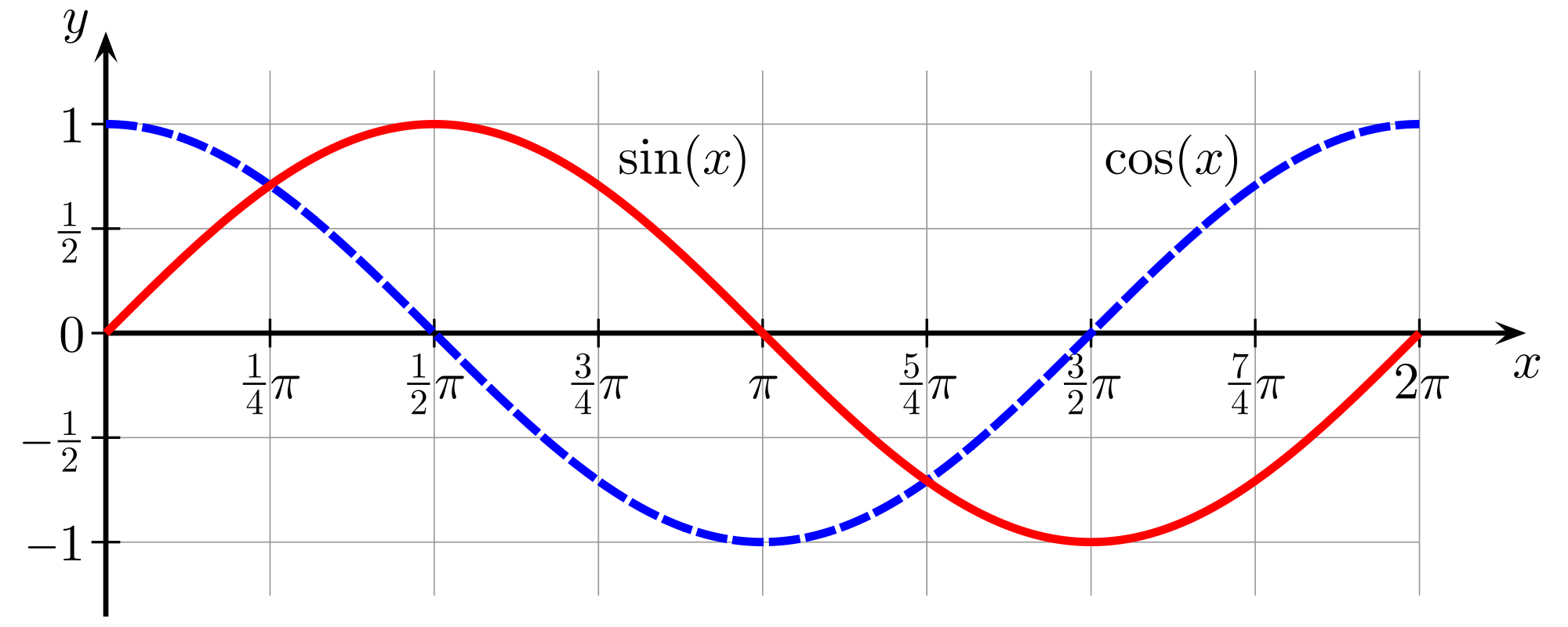
Step 2: Drawing the Basic Sine Wave

To graph the basic sine function:
- Start at the origin (0,0) since sin(0) = 0.
- Move upwards to reach the maximum amplitude, which is typically set at y = 1, at θ = π/2 or 90 degrees.
- Then, come back down to the x-axis at θ = π or 180 degrees where sin(π) = 0.
- Continue down to the negative peak at y = -1 when θ = 3π/2 or 270 degrees.
- Finally, return to the x-axis at θ = 2π or 360 degrees, completing one full cycle.
Step 3: Drawing the Basic Cosine Wave

Graphing cosine is very similar to sine but with a phase shift:
- Begin at the maximum point y = 1 since cos(0) = 1.
- Come down to the x-axis at θ = π/2 or 90 degrees where cos(π/2) = 0.
- Reach the negative peak at y = -1 at θ = π or 180 degrees.
- Move back up to zero at θ = 3π/2 or 270 degrees.
- Finish the cycle at y = 1 when θ = 2π or 360 degrees.
Step 4: Labeling Your Graph
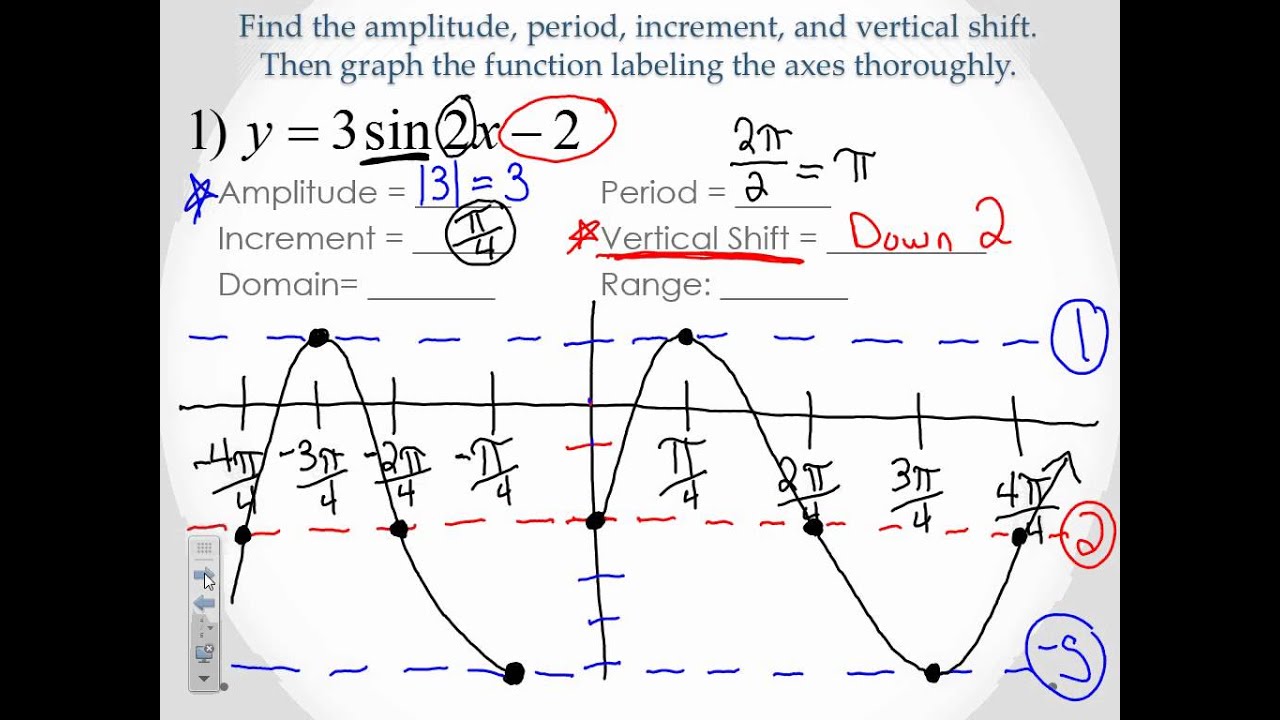
Your graph should now show one complete cycle for sine and cosine:
- Label the x-axis with θ in radians or degrees, ensuring you include π/2, π, 3π/2, and 2π.
- Label the y-axis from -1 to 1, indicating the amplitude.
- Use different colors or line styles to distinguish between sine and cosine if necessary.
💡 Note: Both sine and cosine graphs will repeat this pattern every 2π, illustrating their periodic nature.
Step 5: Recognizing Key Features
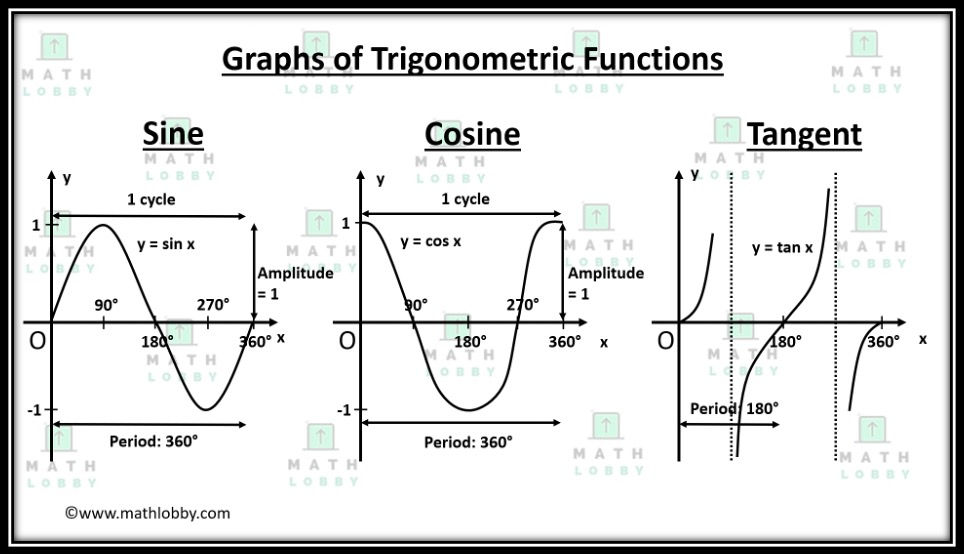
Understanding the following will help in manipulating sine and cosine graphs:
- Amplitude: The peak-to-peak height of the wave. For basic sine and cosine, this is 1.
- Period: The length of one complete cycle, which is 2π for standard sine and cosine functions.
- Phase Shift: Moving the graph left or right without changing its shape.
- Vertical Shift: Moving the graph up or down, which shifts the central axis from the x-axis.
🌐 Note: Trigonometric functions like sine and cosine are foundational in physics to model wave phenomena, electrical engineering for signal processing, and many other fields.
Graphing sine and cosine functions not only enhances your understanding of these mathematical concepts but also equips you to visualize and solve real-world problems where periodic behavior is key. The simplicity and elegance of these functions make them a fascinating subject to explore. By following these steps, you now have the tools to graph these functions accurately and interpret their characteristics with confidence.
Why do we use radians instead of degrees?
+
Radians are used in mathematical applications because they simplify many equations in calculus and trigonometry. The use of π in calculations provides more intuitive insights into the relationships between angles and circular measurements.
How can I remember the sine and cosine values for key angles?

+
One effective method is using the mnemonic “Silly Sally Swiftly Shuffled Sheep” for 0, 30, 45, 60, and 90 degrees respectively, where S corresponds to 0 or 360 degrees where sine is 0, S to 90 degrees where sine is 1, etc. Alternatively, the unit circle can be visualized to remember these values.
What are the practical applications of sine and cosine graphs?
+
Sine and cosine functions are used in acoustics to describe the behavior of sound waves, in electronics for alternating current (AC), in civil engineering to calculate distances and angles, in architecture for curve designs, and many other fields where periodic phenomena occur.