Master Graphing Piecewise Functions with Our Worksheet

Understanding piecewise functions is fundamental in mathematics, especially as you progress from basic algebra to more advanced calculus topics. These functions, which are defined by multiple sub-functions over specific intervals, can be challenging at first. However, mastering them can unlock a deeper understanding of how different mathematical concepts connect. This comprehensive guide will walk you through everything you need to know about graphing piecewise functions, using an interactive worksheet to make the learning process engaging and effective.

What Are Piecewise Functions?

Piecewise functions are mathematical expressions that behave differently on different intervals of the domain. They are essentially a collection of functions patched together to form a single function:

• The pieces are typically defined by the intervals they cover, with each piece usually being a simple polynomial, linear, or another basic function.
• Each segment’s definition includes its own domain, making the overall function’s graph segmented.

Graphing Piecewise Functions

The process of graphing piecewise functions involves several key steps:

1. Identify the Intervals

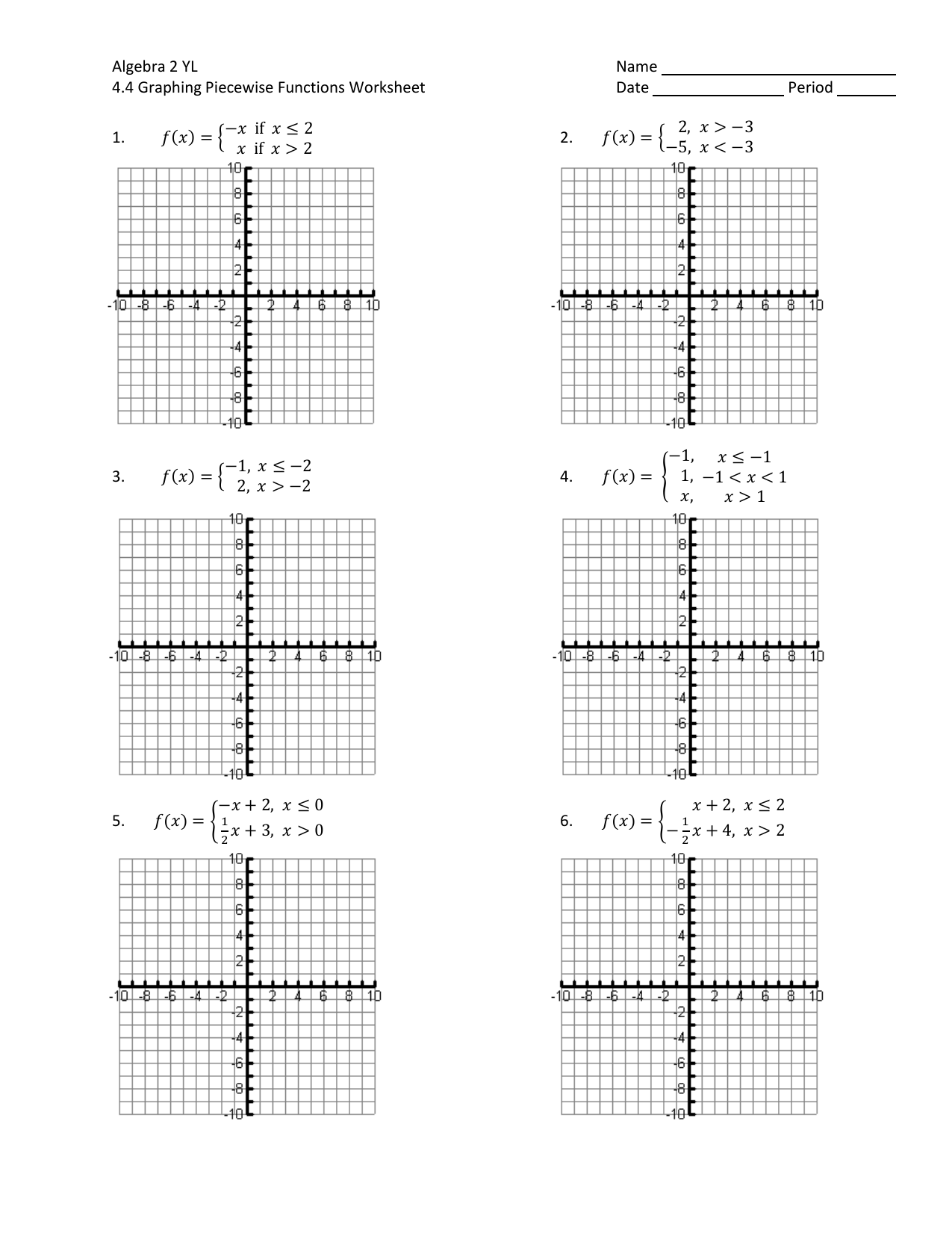
Start by noting the intervals on which each piece of the function is defined. For instance, a piecewise function might be defined as:

f(x) = {
    2x - 1, if x <= 0
    x^2 + 3, if 0 < x < 2
    4, if x >= 2
}

Here, you have three intervals: negative infinity to zero, zero to less than 2, and 2 to positive infinity.

2. Graph Each Piece Separately

For each interval:

• Plot the points from the domain.
• Sketch the function’s behavior on that interval, using a solid dot if the endpoint is included, or an open dot if it’s not.

3. Use Open and Closed Circles

To indicate where a function starts or ends:

• Use a closed circle (•) if the value at that point is included.
• Use an open circle (○) if the value is not included.

Remember, one function’s endpoint must connect smoothly with the next function’s start.

4. Combine the Graphs

After graphing each segment separately:

• Combine the graphs into a single coherent diagram, ensuring that you don’t skip any part of the domain.
• Ensure that the transitions between the segments are clear.

5. Verify Endpoints and Continuity

Check for:

• The function’s value at the interval boundaries (e.g., at x=0 in our example).
• If the function is continuous or jumps at those points.

📌 Note: Always double-check that the piece of the function defined for a specific interval is sketched correctly. Misinterpreting the endpoints can lead to incorrect graphs.

Using a Worksheet for Practice

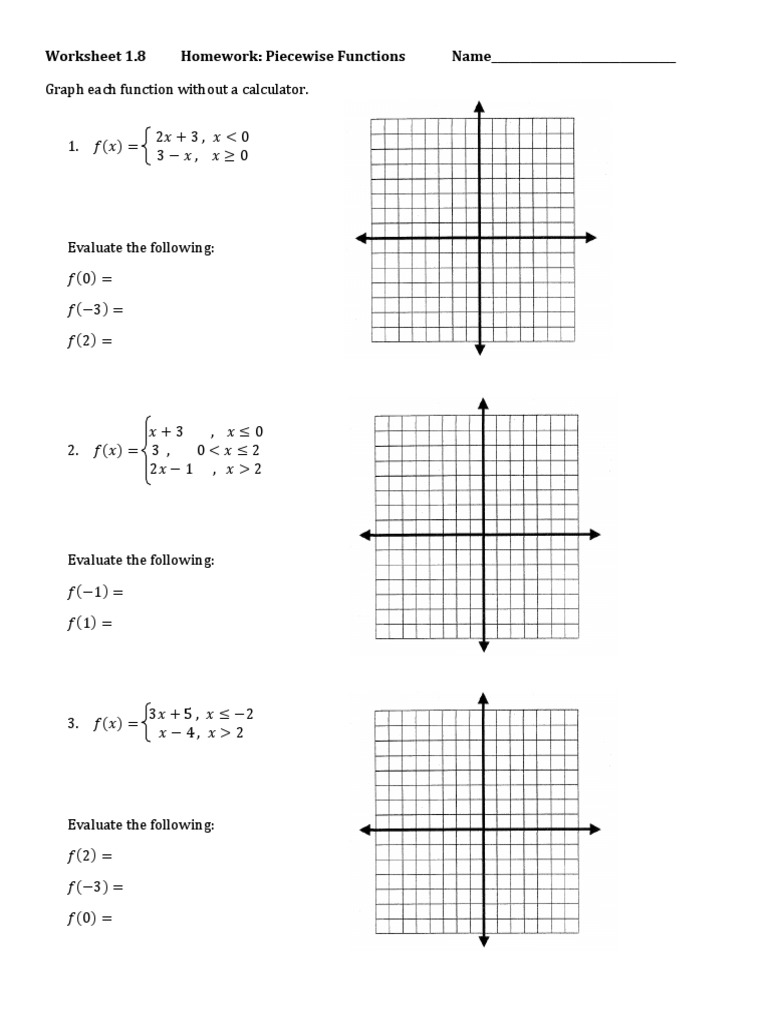
A well-crafted worksheet can be an excellent tool for mastering piecewise functions:

Sample Problem: Graphing a Piecewise Function

Consider the function:

g(x) = {
    x + 2, if x < 1
    -x, if 1 <= x < 3
    2, if x >= 3
}

Graphing Steps:

1. Identify the intervals: (-∞, 1), [1, 3), and [3, ∞).
2. Graph each piece:
   • For x + 2 from negative infinity to less than 1, use a solid dot at (1, 3) and an arrow to represent the function extends left.
   • For -x from 1 to less than 3, connect (1, -1) to (3, -3) with an open dot at (3, -3).
   • At x=3, draw a line at y=2 to represent a constant function, use a solid dot.
3. Use open and closed circles:
   • At x=1, there’s a closed dot from the first piece and an open dot from the second.
   • At x=3, there’s an open dot from the second piece and a solid dot from the third.
4. Verify continuity and endpoints:
   • There’s a jump at x=3, so the function is discontinuous at this point.
   • At x=1, the function switches smoothly from the first to the second piece.

Here's a visual representation of the function:

Benefits of Using a Worksheet

• Provides structured practice with clear expectations.
• Helps visualize the connection between different mathematical concepts.
• Reinforces understanding through practical application.
• Allows for immediate feedback on graphing techniques.

In summary, mastering piecewise functions through practical graphing exercises not only sharpens your mathematical skills but also opens doors to understanding more complex algebraic and calculus concepts. By following the detailed steps outlined in this guide and engaging with a worksheet, you can confidently graph any piecewise function you encounter.

How do I know where to place open or closed dots?

+

An endpoint is included in a function if it’s equal to or greater than (≥) or less than or equal to (≤) the interval’s boundary. Use a closed circle (•) at these points, and use an open circle (○) if the point is not included.

Can piecewise functions have more than two pieces?

+

Yes, piecewise functions can be defined with as many pieces as needed to cover different parts of the domain.

What does it mean if a piecewise function has a jump at an endpoint?

+

A jump indicates a discontinuity where the function abruptly changes value. This could mean the limit does not exist or is different from the value of the function at that point.

How can I ensure that my graph is accurate?

+

By checking that each piece is drawn for its specific interval, ensuring correct endpoints, and verifying continuity or jumps, you can ensure accuracy in graphing.