5 Essential Tips for Solving Absolute Value Equations Graphically

When tackling the complexities of mathematical problems like absolute value equations, understanding how to solve them graphically can offer a visual perspective that's both intuitive and effective. Here, we will explore five essential tips for mastering this approach, ensuring a solid grasp on solving absolute value equations through graphical methods.
Understanding Absolute Value Graphically

To begin, let's delve into what an absolute value represents graphically. The absolute value function, denoted by |x|, essentially strips away the sign, giving the distance a number is from zero on the number line. Here's how we visualize this:
- The graph of |x| is a V-shaped curve starting at the origin (0,0).
- For x < 0, the graph reflects across the y-axis, but for all intents and purposes, the absolute value equation changes to its positive counterpart.

💡 Note: This V-shape indicates that the function does not distinguish between positive and negative values; it's only about the distance from zero.
1. Identifying Key Points

Before attempting to solve absolute value equations graphically, identify the key points:
- The point where the equation intersects the x-axis (where |x| = c).
- The vertex of the V-shape, which is always at (0,0) for basic absolute value functions.
These points are crucial because they provide insights into where the equation equals zero, which is essential for graphical solution.
2. Plotting the Equation

Here's how to plot the graph of an absolute value equation:
- Set the inside of the absolute value equal to zero to find potential points of interest.
- Solve for the values inside to get positive and negative roots.
- Plot these points on a coordinate plane, ensuring to reflect the negative root across the y-axis.
- Connect the points to form the characteristic V-shape of the absolute value function.
3. Determining Intersections
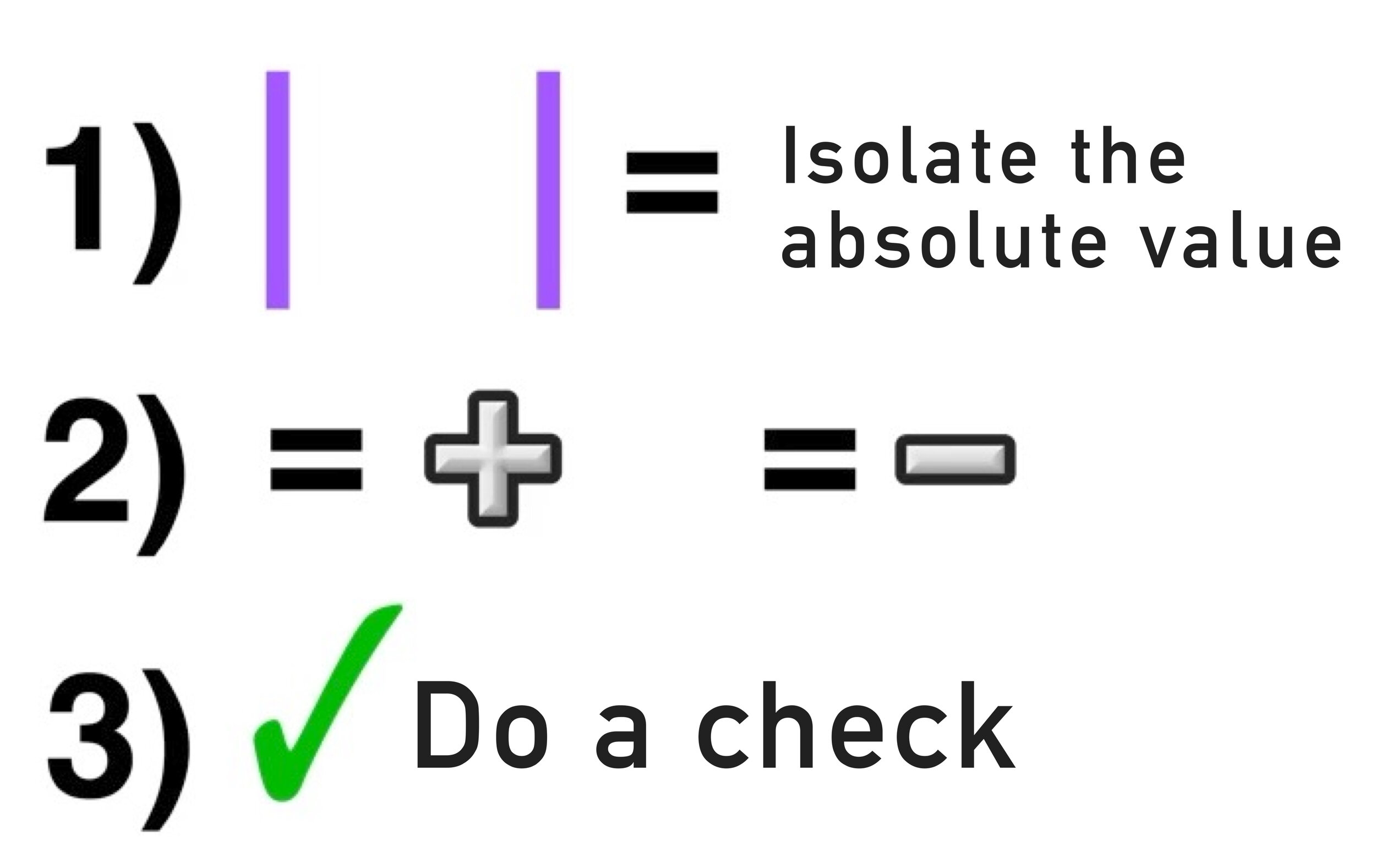
When solving absolute value equations, your goal is to find where two graphs intersect:
- The graph of the absolute value equation |x| = c.
- Another graph, perhaps a linear equation y = c, where c is a constant.
To solve:
- Plot both functions on the same coordinate system.
- Identify the points where they intersect, which are your solutions.
4. Using Inequalities to Find Ranges

Absolute value equations often come with inequalities, like |x| < c or |x| > c:
- If |x| < c, the solutions lie between two points on the x-axis where the absolute value graph crosses the line y = c.
- If |x| > c, the solutions are outside of these two points, encompassing all values where the graph is above or below the line y = c.
5. Advanced Techniques

For more complex absolute value equations, consider these advanced techniques:
- Transformations: Understand how transformations affect the graph, such as vertical and horizontal shifts or stretches.
- Systems of Equations: Solve systems involving absolute value equations, where you might need to graph two or more functions and find where they overlap.
These techniques can expand your problem-solving toolkit and help you visualize solutions in more intricate scenarios.
Lastly, we wrap up with a summary of what we've learned about graphically solving absolute value equations:
In summary, mastering the art of solving absolute value equations graphically involves understanding the absolute value function's V-shape, identifying key points, plotting equations, determining intersections, handling inequalities, and employing advanced techniques like transformations and systems of equations. Each tip provides insight into how visual cues can guide us to the correct solutions, making this method both intuitive and efficient for tackling such equations.
Can absolute value equations always be solved graphically?

+
Yes, provided you can accurately plot the graph of the absolute value function and any other equation involved. Graphical solutions work well for visualizing where equations intersect or overlap, though numerical or algebraic methods might be necessary for more precision.
How does the value of ‘c’ affect the graph in |x| = c?

+
The value of ‘c’ determines the height at which the absolute value graph intersects the y-axis or where the equation equals zero. For example, if |x| = 2, the graph intersects the line y = 2 at x = ±2.
What happens if the absolute value graph doesn’t intersect the other equation?

+
If there’s no intersection, it means there’s no real solution to the equation. The two functions never meet on the coordinate plane.