7 Ways to Master Similar Triangles in Geometry

Understanding the Concept of Similar Triangles
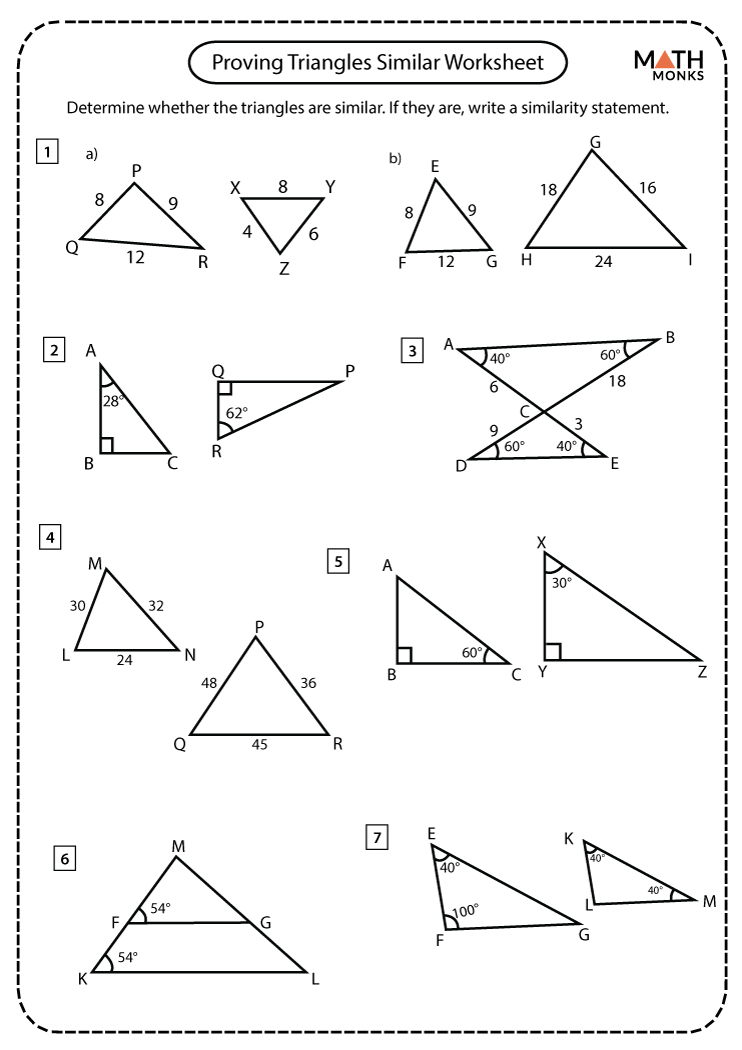
Similar triangles are a fundamental concept in geometry where two triangles are said to be similar if they have the same shape but not necessarily the same size. This similarity is based on three key conditions:
- Angle-Angle (AA) Similarity: If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar.
- Side-Side-Side (SSS) Similarity: If the ratios of the corresponding sides of two triangles are equal, the triangles are similar.
- Side-Angle-Side (SAS) Similarity: If one angle of a triangle is congruent to one angle of another triangle and the sides including those angles are proportional, the triangles are similar.
Understanding these conditions helps in solving many geometric problems where similarity plays a crucial role in maintaining proportional relationships within triangles.
🔍 Note: While understanding these similarity criteria is crucial, students often find the practical application of these rules challenging. Recognizing the conditions early in your problem-solving process will simplify the geometric operations.
Visualizing Similar Triangles

To effectively understand similar triangles, visual aids can be very beneficial:

- Corresponding Angles: Highlight or mark the angles that are congruent in both triangles. This visual cue immediately shows why triangles are similar under the AA criterion.
- Proportional Sides: Use different colors or line styles to show which sides are proportional. This helps in understanding the SSS and SAS similarity criteria visually.
- Scaling: Display one triangle next to a scaled version of the other to visually grasp the concept of similarity without needing exact measurements.
👁️ Note: Visualization aids not only help in understanding but also in retaining the concepts better. Always try to draw or use diagrams when solving problems involving similar triangles.
Methods to Prove Triangle Similarity

Proving that two triangles are similar requires a clear understanding and application of similarity criteria:
| Method | Description | When to Use |
|---|---|---|
| AA (Angle-Angle) | Two triangles are similar if two of their corresponding angles are equal. | Use when you know or can deduce the measure of two angles in both triangles. |
| SSS (Side-Side-Side) | The ratios of the lengths of the corresponding sides are equal. | Ideal when you have the lengths of all sides or can calculate them proportionally. |
| SAS (Side-Angle-Side) | Two triangles are similar if one angle of one triangle is congruent to one angle of the other, and the sides including these angles are proportional. | Useful when you have a known angle and two corresponding sides. |

📚 Note: Each method has its strengths. Recognizing which method to apply can streamline your proofs and save time during exams or problem-solving sessions.
Real-World Applications of Similar Triangles

Similar triangles are not just theoretical constructs; they have numerous practical applications:
- Architecture: Architects use the principles of similarity to design buildings or structures with proportional scaling, ensuring aesthetic balance.
- Surveying: Surveyors use similar triangles to calculate distances or heights of inaccessible points by creating similar triangles and using their known lengths.
- Computer Graphics: In 3D modeling, understanding similar triangles helps in rendering correct proportions and perspectives of objects on the screen.
- Navigation: Pilots and sailors use triangulation, which relies on similar triangles, to calculate their position relative to known landmarks.
Each application illustrates how the concept of similar triangles can be adapted to solve real-world problems efficiently and accurately.
Strategies for Solving Problems Involving Similar Triangles

Solving geometry problems involving similar triangles requires a structured approach:
- Identify Similarity: Begin by determining whether the triangles involved are similar by applying one or more of the similarity criteria.
- Set Up Proportions: If triangles are similar, set up ratios of corresponding sides. For example, if triangles ABC and DEF are similar, you might write AB/DE = BC/EF = AC/DF.
- Solve for Unknowns: Use the established proportions to find unknown lengths or angles. Cross-multiplying often helps in solving these proportions.
- Double-Check: After solving, verify your answers by re-applying the similarity criteria or using alternative methods if available.
🧮 Note: Cross-checking your work with multiple methods not only reinforces your understanding but also helps catch any initial mistakes in problem-solving.
Common Pitfalls and How to Avoid Them

There are several common mistakes students make when dealing with similar triangles:
- Confusing Similarity with Congruence: Remember, congruence means triangles are the same in shape and size, whereas similarity means they have the same shape but can differ in size.
- Improper Use of Proportions: Always set up the correct proportions when using the side-side-side or side-angle-side methods. Misaligning sides or angles will lead to incorrect answers.
- Ignoring Non-Given Angles: Sometimes, students miss out on using the sum of angles in a triangle being 180 degrees to find unknown angles, which could simplify the problem significantly.
Advanced Topics and Further Exploration
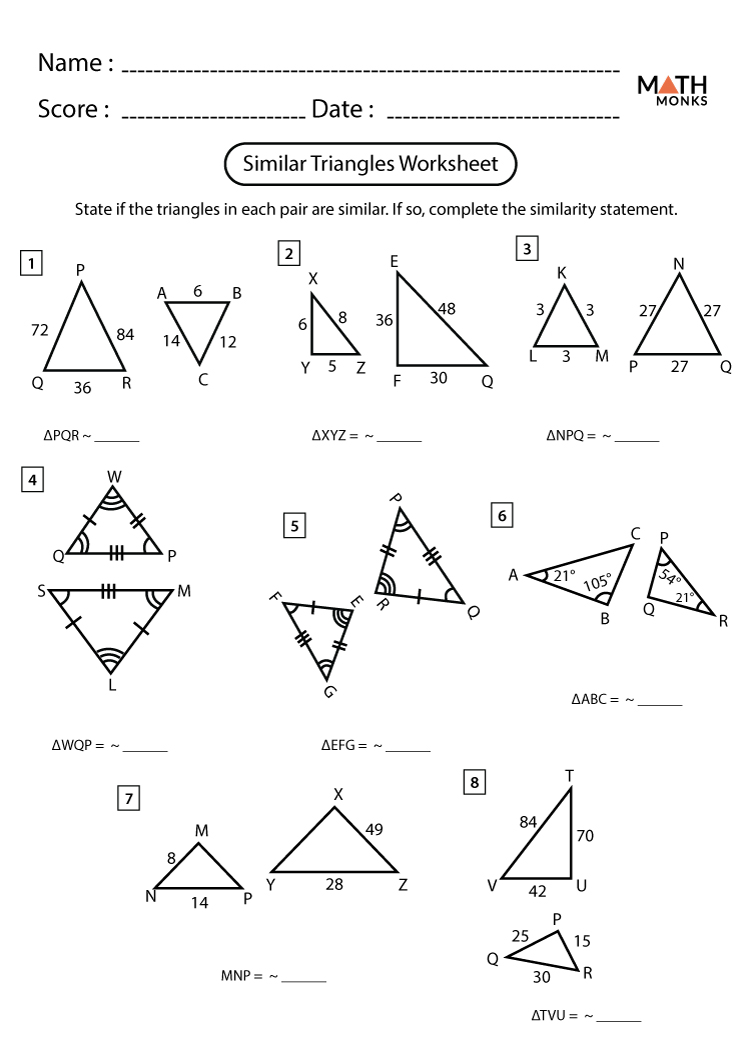
Once you've mastered the basics, you might want to delve into more complex applications:
- Trigonometry in Similar Triangles: Explore how the trigonometric ratios (sine, cosine, tangent) can be used when dealing with angles in similar triangles.
- Dilation and Transformation: Understand how similar triangles relate to transformations like dilation where every segment is scaled by a constant factor.
- Non-Euclidean Geometry: Similar triangles in hyperbolic or spherical geometry can open up new realms of understanding and problem-solving.
Exploring these areas will enhance your grasp of similar triangles and how they integrate into broader geometric and mathematical contexts.
Summing up, mastering similar triangles involves understanding their criteria, visualizing their properties, applying practical methods to prove similarity, appreciating their real-world applications, strategizing problem-solving approaches, avoiding common pitfalls, and exploring advanced topics. By internalizing these strategies, geometry becomes not just a subject of study but a tool for logical analysis and visual thinking, enhancing your ability to solve complex problems with elegance and efficiency.
What is the easiest way to check if two triangles are similar?

+
The Angle-Angle (AA) criterion is often the simplest because if you can confirm that two angles in one triangle are congruent to two angles in another, the triangles are similar by default.
Can triangles be similar if they have two sides proportional but different angles?

+
No, for triangles to be similar, the corresponding sides must be proportional and the corresponding angles must be congruent.
How does similarity affect the area of triangles?

+
The ratio of the areas of two similar triangles is the square of the ratio of their corresponding sides. If one side of a triangle is k times the corresponding side of the other, the areas differ by k².