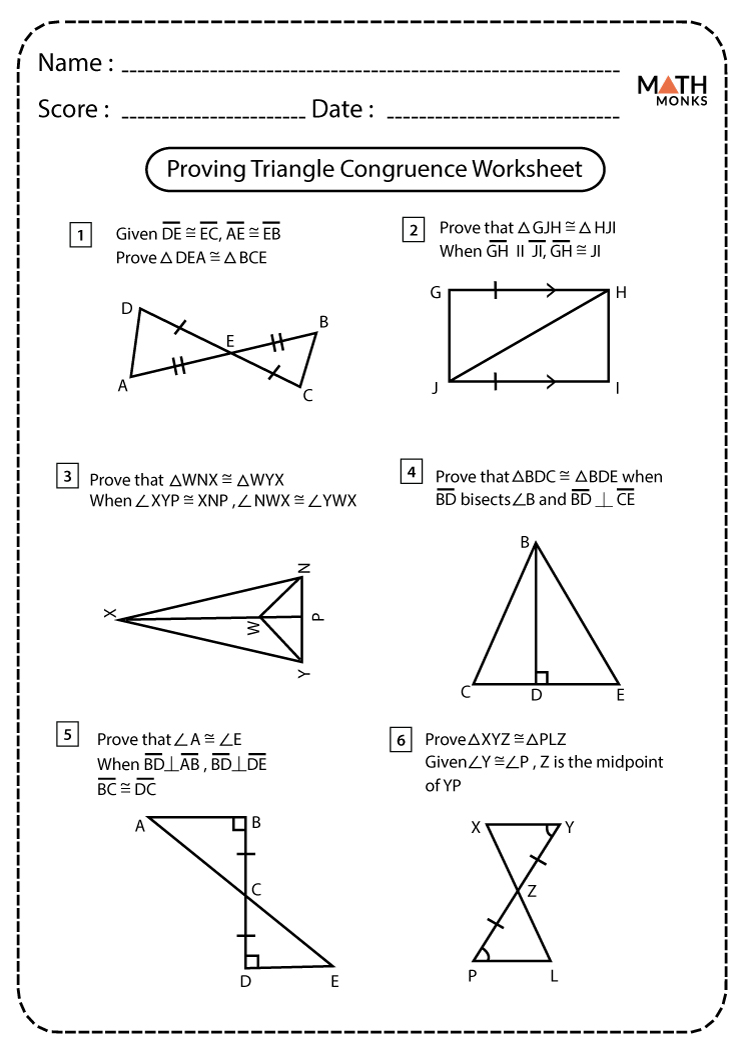
5 Essential Triangle Proofs in Geometry Worksheets

In the vast world of geometry, triangle proofs hold a special place due to their fundamental importance in understanding geometric principles. Working through triangle proofs not only improves one's logical reasoning but also prepares students for more advanced topics in mathematics and real-world problem-solving. This blog post explores five essential triangle proofs commonly found in geometry worksheets, detailing their significance, how to approach them, and why they matter in the study of geometry.
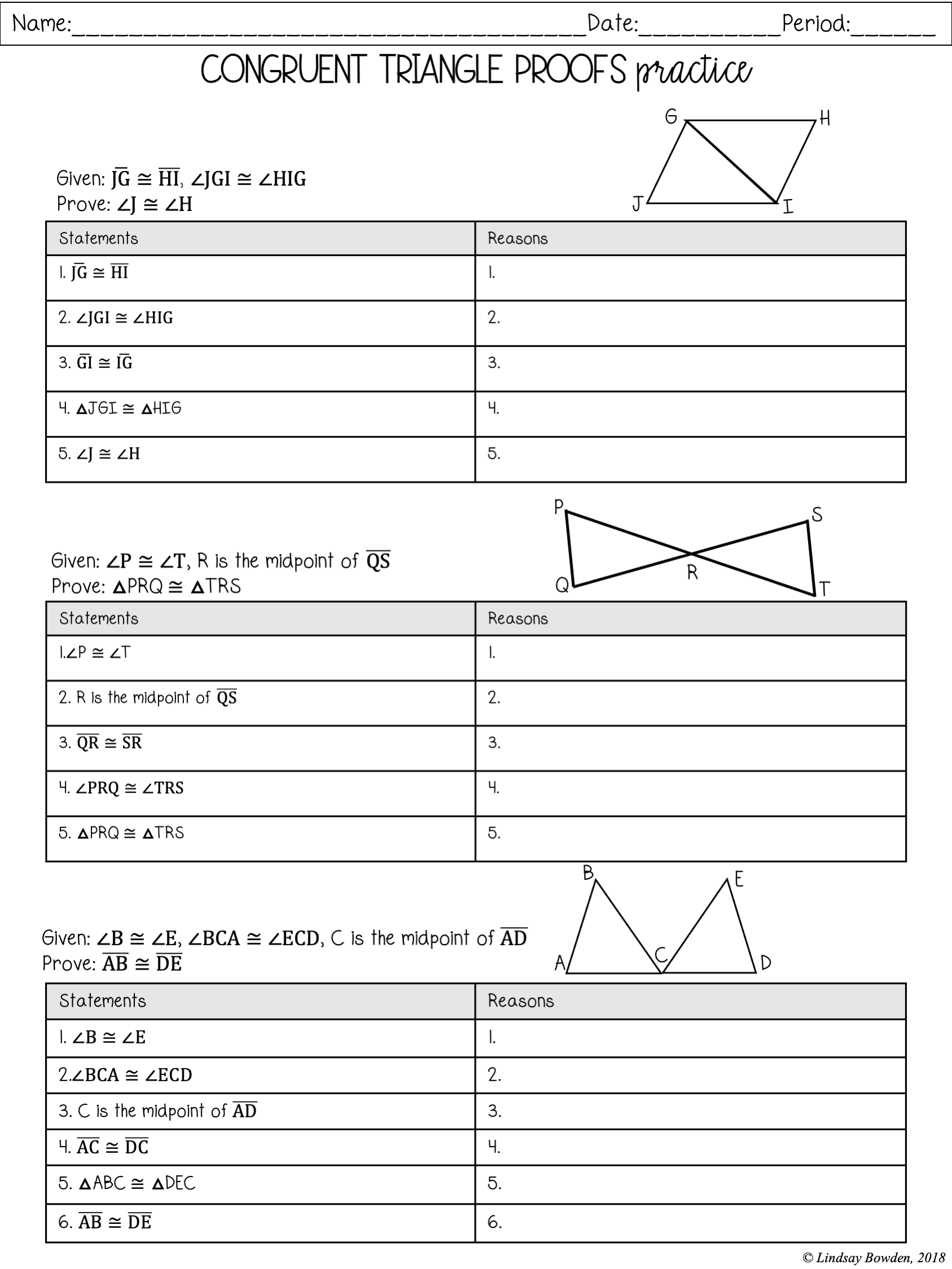
Congruent Triangles and Their Proofs

Congruent triangles form the backbone of many geometric proofs. Here are the key methods for proving triangle congruency:
- Side-Side-Side (SSS): If all three sides of one triangle are equal in length to the three sides of another triangle, the triangles are congruent.
- Side-Angle-Side (SAS): If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, the triangles are congruent.
- Angle-Side-Angle (ASA): If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, the triangles are congruent.
- Angle-Angle-Side (AAS): If two angles and a non-included side of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
- Hypotenuse-Leg (HL) for Right Triangles: If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, the triangles are congruent.
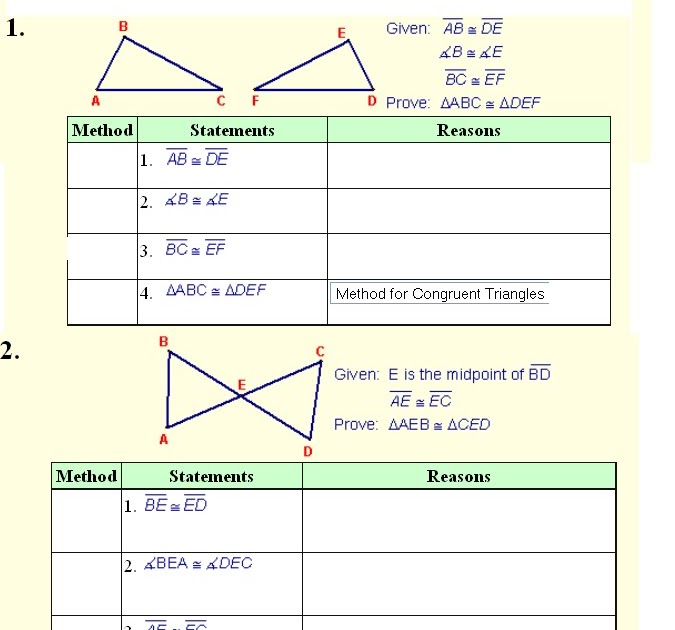
Example of a Triangle Congruency Proof
To illustrate, let's examine an example using the SAS method:
| Step | Description |
|---|---|
| 1 | Given: ΔABC and ΔDEF where AB = DE, AC = DF, and ∠A = ∠D |
| 2 | To Prove: ΔABC ≅ ΔDEF |
| 3 | Proof:
|
| 4 | By the SAS criterion, ΔABC is congruent to ΔDEF |
🔍 Note: Students often confuse ASA and AAS. Remember, ASA uses the included side, whereas AAS uses any side.
Similarity and Proportionality in Triangles

Triangle similarity is another crucial aspect. Here’s how triangles can be proven similar:
- AA (Angle-Angle): If two angles of one triangle are equal to two angles of another triangle, then the triangles are similar.
- SAS (Side-Angle-Side) Similarity: If an angle of one triangle is congruent to an angle of another triangle and the lengths of the sides including these angles are proportional, the triangles are similar.
- SSS (Side-Side-Side) Similarity: If corresponding sides of two triangles are proportional, the triangles are similar.
Triangle Similarity Example
Consider the following example using the AA method:
| Step | Description |
|---|---|
| 1 | Given: ΔPQR and ΔSTU where ∠P = ∠S, ∠Q = ∠T |
| 2 | To Prove: ΔPQR ~ ΔSTU |
| 3 | Proof:
|
| 4 | By the AA criterion, ΔPQR is similar to ΔSTU |
Isosceles Triangle Theorem and Its Proof

The Isosceles Triangle Theorem states that if two sides of a triangle are congruent, then the angles opposite those sides are congruent. Here’s how to prove it:
- Base Angles Theorem: If AB = AC, then ∠B = ∠C.
- Converse: If ∠B = ∠C, then AB = AC.
Isosceles Triangle Proof
To prove the base angles theorem:
| Step | Description |
|---|---|
| 1 | Given: ΔABC with AB = AC |
| 2 | To Prove: ∠B = ∠C |
| 3 | Proof:
|
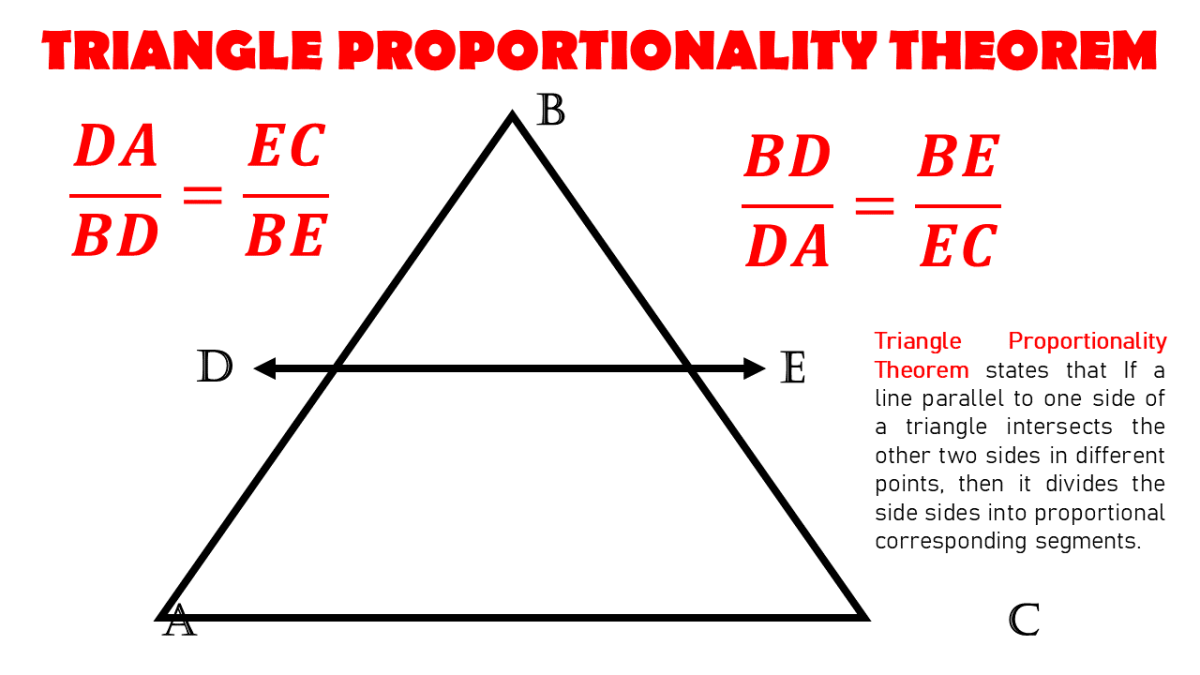
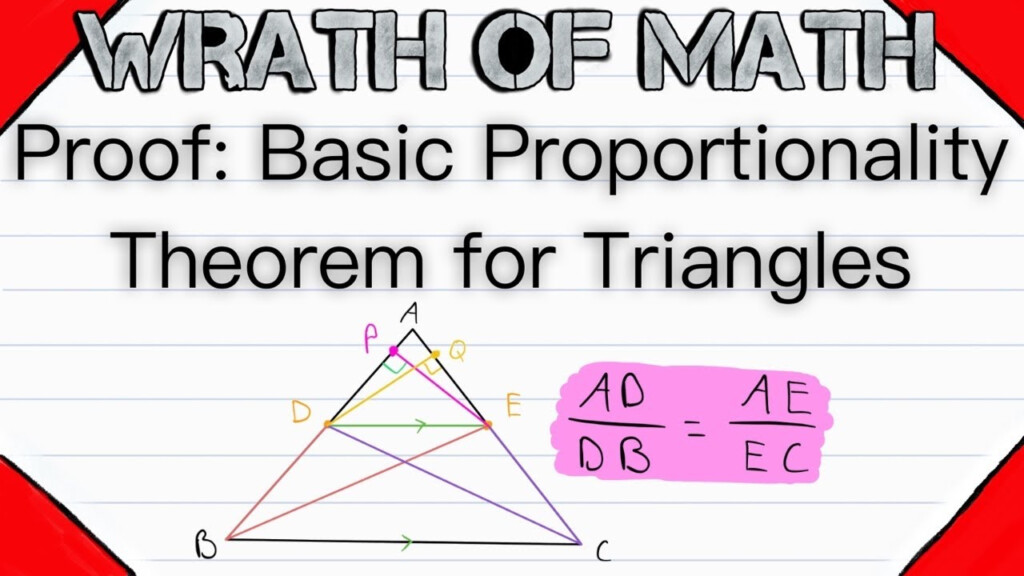
Triangle Midsegment Theorem
The midsegment (or midline) of a triangle connects the midpoints of two sides of the triangle. The Midsegment Theorem states that:
- The midsegment is parallel to the third side and half its length.
Midsegment Theorem Proof

Here’s how to prove the midsegment theorem:
| Step | Description |
|---|---|
| 1 | Given: ΔABC with midpoints D on AB and E on AC |
| 2 | To Prove: DE is parallel to BC and DE = ½BC |
| 3 | Proof:
|
Pythagorean Theorem

The Pythagorean theorem is a cornerstone of geometric proof, expressing a fundamental relationship between the legs and the hypotenuse of a right triangle:
- If (a) and (b) are the lengths of the legs, and (c) is the hypotenuse, then (a^2 + b^2 = c^2).
One Proof of the Pythagorean Theorem
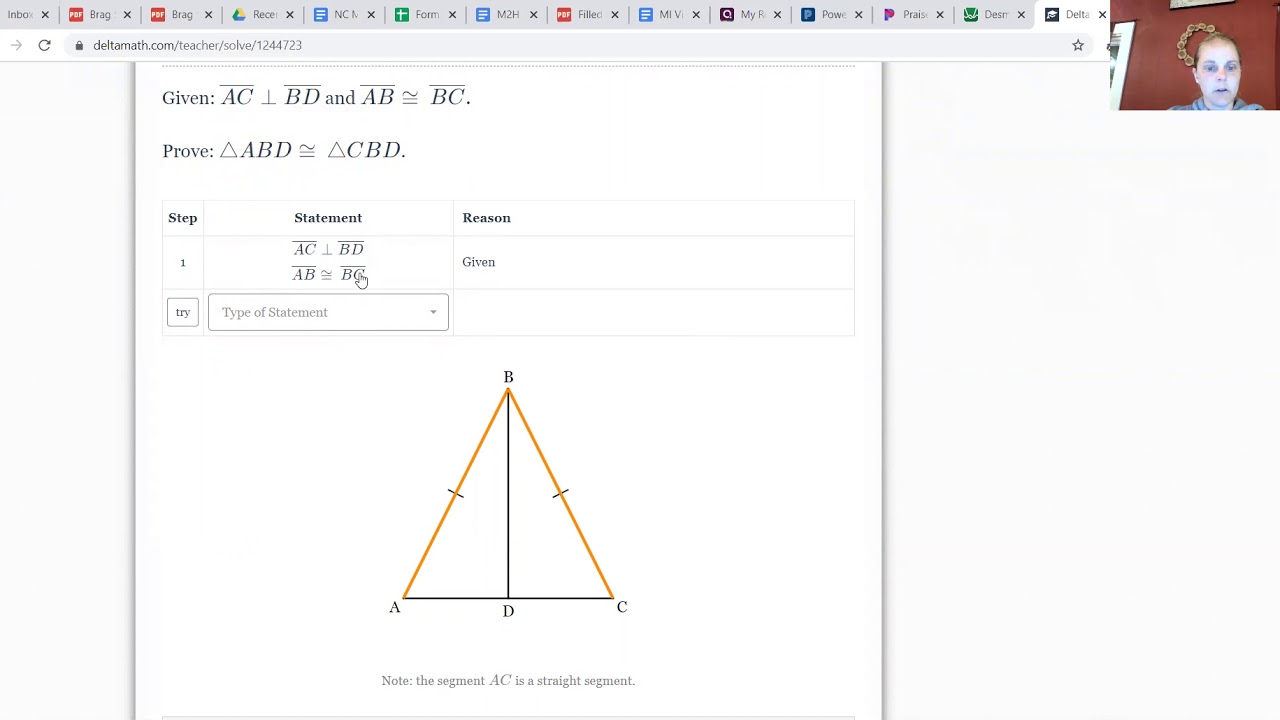
Here is one common geometric proof of the theorem:
| Step | Description |
|---|---|
| 1 | Given: Right triangle ABC with the right angle at A |
| 2 | To Prove: (a^2 + b^2 = c^2) |
| 3 | Proof:
|
💡 Note: There are several different proofs for the Pythagorean theorem, each with its own unique approach.
Wrapping up these five key triangle proofs provides a robust foundation in geometry, equipping students with the tools to tackle a variety of geometric problems. These proofs not only demonstrate the logical coherence of geometric principles but also foster critical thinking, problem-solving skills, and an appreciation for the beauty of mathematical structure. Mastery of these fundamental proofs opens the door to more complex geometric inquiries, making geometry an engaging and deeply insightful subject.
Why are triangle proofs important in geometry?
+
Triangle proofs are essential because they help establish the foundational theorems and axioms upon which many geometric properties depend. They enhance logical reasoning and problem-solving abilities, providing a structured way to understand and verify geometric relationships.
How can I remember the difference between ASA and AAS?
+
The mnemonic for ASA is “Angle, Side, Angle,” focusing on the included side between the two angles. For AAS, remember “A-An-Angle” where the side is non-included.
What is the most straightforward triangle proof for students?
+
The SSS or SAS proofs are often the easiest to start with due to their straightforward nature. They involve comparing sides or sides and angles, which is easier for students to visualize and understand.
Can triangle similarity theorems be applied to all triangles?

+
Yes, triangle similarity theorems can be applied to all triangles. However, they are most frequently used with non-right triangles, as right triangles often involve specific proofs related to their unique properties.
Are there real-world applications of triangle proofs?

+
Indeed, triangle proofs underpin many practical fields. For example, in construction, they’re used to ensure structural stability; in computer graphics, they help in rendering shapes; and in navigation, they’re crucial for calculations in triangulation.