Geometry Transformation Composition Worksheet Answer Key Revealed

Welcome to our comprehensive guide on understanding the answer key for geometry transformation composition worksheets. This educational exploration is crafted to enhance your understanding of how to solve various geometric transformation problems, particularly those involving composition or sequences of transformations.
Understanding Basic Transformations
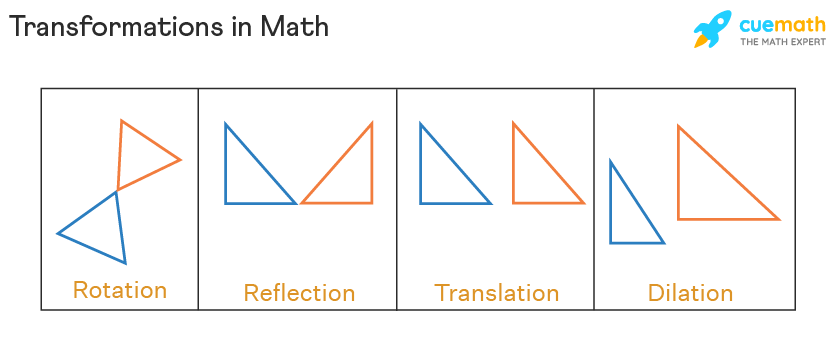
Before diving into the composition, let’s briefly outline the basic transformations in geometry:
- Translation: Moving an object from one position to another without changing its size, shape, or orientation.
- Reflection: Flipping an object over a line, called the line of reflection, to create a mirror image.
- Rotation: Turning an object around a fixed point by a specific angle, often using degrees as a unit of measure.
- Dilation: Scaling an object by changing the distances from the center of dilation, making the object larger or smaller without altering its shape or orientation.
Composition of Transformations

The composition of transformations involves performing multiple transformations on a geometric figure in a specific sequence. Here’s how to approach such problems:
- Identify the Order: The sequence matters as each transformation impacts the next. Read the problem carefully to identify which transformations need to be applied in what order.
- Apply Each Transformation:
- For translation, add or subtract coordinates.
- Reflect over the specified line using rules like (x, y) -> (-x, y) for vertical reflection.
- Rotate around the origin or a specific point using trigonometric functions or coordinate rules.
- Multiply the coordinates by the scale factor for dilation.
- Track the Resulting Coordinates: After each transformation, calculate the new coordinates and use them for the next transformation.
Here is an example with step-by-step calculations:
| Transformation | Starting Coordinates | New Coordinates |
|---|---|---|
| Translation (Move 2 units right, 3 units up) | (2, 4) | (4, 7) |
| Reflection (Over x-axis) | (4, 7) | (4, -7) |
| Rotation (90 degrees counterclockwise around origin) | (4, -7) | (7, 4) |

🌟 Note: Keep track of all coordinates after each transformation to avoid mistakes in your final answer.
Practice Problems with Answers

Let’s delve into some practice problems with their respective answers:
Problem 1: Translation then Rotation

A point at (3, 1) is translated 5 units right and 2 units down, then rotated 45 degrees clockwise around the origin. Find the final coordinates.
- Translate: New coordinates are (8, -1).
- Rotate: Using rotation formulas, the final coordinates are approximately (-2.12, 4.12).
Problem 2: Dilation then Reflection

A triangle with vertices at A(2, 2), B(4, 4), and C(6, 2) is dilated by a scale factor of 3 with the origin as the center, then reflected over the y-axis. Find the new vertices.
- Dilate: Vertices become A(6, 6), B(12, 12), and C(18, 6).
- Reflect: The new vertices are A(-6, 6), B(-12, 12), and C(-18, 6).
📌 Note: Always check your results by drawing or verifying with coordinate calculations.
The Role of Technology in Geometry Composition

Using software like GeoGebra or graphing calculators can significantly enhance the visualization and verification process for geometric transformations:
- These tools allow you to simulate transformations in real-time.
- You can verify your answers by plotting the points and applying transformations step by step.
- Visual aids can help in understanding how each transformation changes the figure’s orientation and position.
At the end of our exploration, we've covered essential strategies and solutions for tackling geometry transformation composition problems. Remember, understanding each transformation individually is key to mastering their composition. Maintaining a clear, logical approach to solving these problems not only ensures accuracy but also improves your problem-solving skills in geometry.
What is the importance of the order in geometric transformation composition?

+
The order of transformations can significantly change the final result of the figure’s position, size, or orientation. For instance, translating a figure before reflecting it will yield a different outcome than reflecting it first and then translating.
How does one ensure accuracy in geometric transformations?

+
Ensure accuracy by:
- Following the correct order of transformations.
- Tracking each set of coordinates precisely.
- Verifying results through drawing or using technology tools.
Can technology tools replace manual calculation?

+
While technology tools like GeoGebra or graphing calculators can verify and simulate transformations, understanding the manual calculation process is still crucial for gaining deep conceptual knowledge and problem-solving skills.