Special Right Triangles: Geometry Worksheet Answers

Right triangles come in various forms and possess unique properties, but none are as captivating and useful as Special Right Triangles. These triangles stand out in the world of mathematics due to their predictable side lengths and angle measurements. Whether you're a student, teacher, or enthusiast of geometry, understanding these special right triangles can not only solve mathematical problems but also offers a glimpse into the fascinating patterns of numbers and shapes.
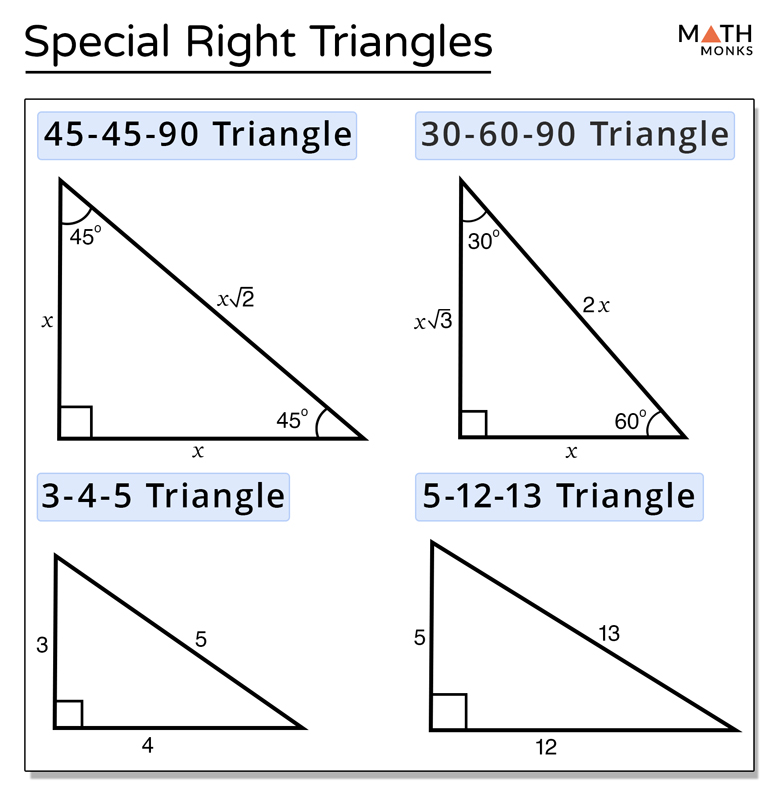
The 45°-45°-90° Triangle

The first of our special triangles is the 45°-45°-90° triangle. This triangle is isosceles and exhibits:
- Two equal angles of 45°
- One right angle of 90°
The ratio of its sides:
- The legs are congruent
- The hypotenuse is √2 times the length of each leg
| Side | Length Ratio |
|---|---|
| Leg 1 | 1 |
| Leg 2 | 1 |
| Hypotenuse | √2 |

How to Solve for Unknown Sides
Imagine you have one side known, let's say the leg:
- If a leg equals x, the hypotenuse is x√2.
- If the hypotenuse equals x, each leg is x/√2 or x/2 (simplified).
🧮 Note: Always rationalize the denominator to simplify your answers.
The 30°-60°-90° Triangle

The 30°-60°-90° triangle has one very special property; it is half of an equilateral triangle:
- One angle at 30°
- Another at 60°
- The third, of course, at 90°
The ratios of its sides are:
- Shortest leg (opposite the 30° angle): 1
- Longer leg (opposite the 60° angle): √3 times the shortest leg
- Hypotenuse: 2 times the shortest leg
| Side | Length Ratio |
|---|---|
| Shortest Leg | 1 |
| Longer Leg | √3 |
| Hypotenuse | 2 |
Finding Unknown Sides

Let’s assume you know the shortest leg:
- The longer leg becomes √3 times the shortest leg.
- The hypotenuse is simply 2 times the shortest leg.
✏️ Note: When calculating, ensure you use exact values when dealing with irrational numbers like √3.
Real-world Applications

These triangles are not just for classroom learning; they have practical applications in various fields:
- Architecture: For designing roofs with different pitches, especially the hip roof, which forms a 45°-45°-90° triangle.
- Surveying: When splitting land or creating right angles, these triangles are pivotal.
- Engineering: Electrical engineers might use these for calculations in trigonometry, especially sine and cosine values for phase shifts in AC circuits.
- Navigation: For example, determining the height of an object when the angle of elevation is known.
In summary, special right triangles simplify many mathematical problems by reducing the need for complex calculations. They teach us not just about angles and lengths but also about the beauty of mathematical patterns. Understanding their ratios can enable quick problem-solving, foster a deeper appreciation for geometry, and provide insight into the application of mathematics in our daily lives. This knowledge is foundational for further explorations in geometry, trigonometry, and beyond.
What makes a triangle a special right triangle?

+
Triangles become special due to their predictable angle measurements and side length ratios, making them easier to work with in mathematical computations.
Can you find a 30°-60°-90° triangle in nature or construction?
+
Yes, in nature, one can observe similar shapes in crystal structures or the patterns in snowflakes. In construction, these triangles are often used for stair designs, roof framing, or as structural components in trusses.
How do I remember the ratios of a special right triangle?

+
Mnemonics like “3-4-5” for the 30°-60°-90° triangle or “1-1-√2” for the 45°-45°-90° triangle can be useful. Visual aids or drawing the triangles frequently also helps in memory retention.