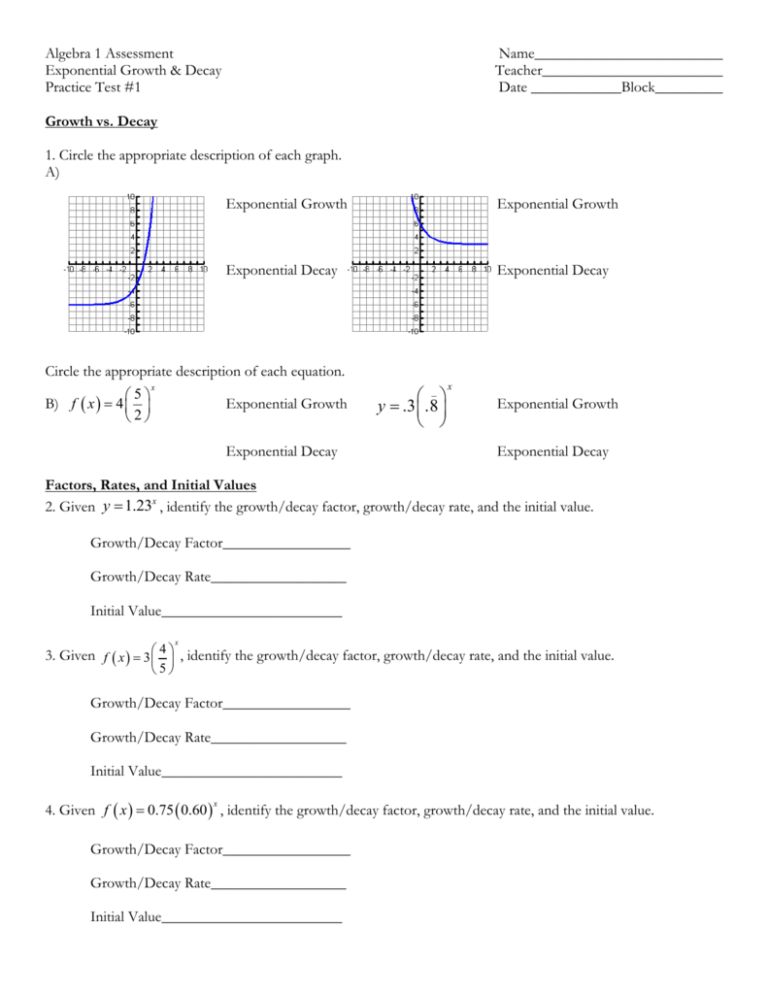
Geometry Segment Addition Worksheet: Answer Key with 5 Tips

Geometry Segment Addition can be a challenging concept for students in their mathematical education. Understanding how to add segments or find the length of segments in various geometric figures not only helps in problem-solving but also fosters a deeper understanding of geometry itself. This post provides an answer key along with 5 essential tips for mastering geometry segment addition, ensuring that students can apply these techniques effectively in their studies.
Segment Addition Postulate

The Segment Addition Postulate states that if three points A, B, and C are collinear such that B lies between A and C, then the length of AB plus the length of BC equals the length of AC. Mathematically, this is written as:
[ AB + BC = AC ]💡 Note: When working with collinear points, ensure all points lie on the same line. Collinearity is crucial for the application of this postulate.
Answer Key

Below is an example of a Geometry Segment Addition Worksheet answer key:
| Problem | Answer |
|---|---|
| 1. Given A, B, C are collinear points such that AB = 12, BC = 8, Find AC | AC = AB + BC = 12 + 8 = 20 |
| 2. If AC = 25 and AB = 16, Find BC | BC = AC - AB = 25 - 16 = 9 |
| 3. Given AC = 40, BC = 20, Find AB | AB = AC - BC = 40 - 20 = 20 |

This answer key helps students check their solutions and understand the logic behind the calculations.
5 Tips for Mastering Segment Addition

Here are some practical tips to enhance your proficiency with segment addition in geometry:
1. Visualize the Problem

- Draw the points on a line to visualize the arrangement and distances.
- Use visual aids to identify which segments form the total length you are looking for.
🔍 Note: Visualization often makes complex problems easier to understand and solve.
2. Understand the Postulate

- Get comfortable with the fact that points on a line can always be added or subtracted in a segment context.
- Remember that this applies only to collinear points.
3. Label Your Points

- Label your points clearly and in order. This avoids confusion when adding or subtracting segment lengths.
- Use letters consistently across problems.
4. Use Algebra to Solve

- Set up equations using the segment addition postulate and solve using algebra.
- Remember that variables like x and y can represent unknown segment lengths.
✨ Note: Integrating algebra with geometry enhances problem-solving skills in both areas.
5. Practice Regularly

- Geometry, like any other math subject, improves with practice. Work on different types of problems daily.
- Seek out additional resources like online worksheets or textbooks for more practice.
Wrapping Up

In mastering geometry segment addition, understanding the Segment Addition Postulate and applying these tips can significantly boost your proficiency. This approach not only helps in solving segment addition problems but also enhances your overall grasp of geometric principles. By visualizing problems, understanding the foundational postulates, properly labeling, using algebra, and practicing regularly, students can confidently tackle geometric challenges.
What is the Segment Addition Postulate?

+
The Segment Addition Postulate states that if three points lie on a straight line, the total length of the line segment between the outer points is the sum of the lengths of the segments between the inner point and the two outer points.
How can visualization help in solving segment addition problems?

+
Visualization aids in understanding the spatial relationships between points, making it easier to apply the Segment Addition Postulate correctly.
Why is it important to label points in segment addition?

+
Labeling points clearly helps in maintaining clarity and avoiding mistakes when calculating segment lengths, especially when working with multiple problems.