Geometry Basics: 5 Simple Worksheet Solutions Explained

Understanding geometry is essential for both academic success and real-life applications. Whether you're figuring out the dimensions of a new furniture piece for your home or measuring land for construction, the fundamental principles of geometry are indispensable. This blog post will guide you through five basic worksheet solutions, explaining each step clearly to enhance your understanding of these concepts.
Area of Rectangles


Calculating the area of rectangles is often one of the first geometry exercises students encounter. Here's how you can solve it:
- Identify the Length and Width: Begin by noting the given dimensions of the rectangle.
- Apply the Formula: Use the formula \text{Area} = \text{length} \times \text{width} . For instance, if a rectangle has a length of 5 units and a width of 3 units, the calculation would look like this:
-
Area = 5 units × 3 units
Area = 15 square units
Perimeter of Squares


Determining the perimeter of a square is straightforward once you know the side length:
- Identify the Side Length: Determine the length of one side of the square.
- Use the Perimeter Formula: Multiply the side length by 4 (since all sides are equal in a square):
Perimeter = 4 × side length
If a side is 7 units, then the perimeter is:Perimeter = 4 × 7
Perimeter = 28 units
Area of Triangles


The area of a triangle can be found using:
- Base and Height: Base × Height divided by 2.
- Example:
- Base = 6 units, Height = 4 units
- Area = (6 units × 4 units) / 2
- Area = 12 square units
Circumference of Circles


The formula for the circumference of a circle involves the radius:
- Use the Formula: \text{Circumference} = 2 \times \pi \times \text{radius}
- If the radius is 3 units:
- Circumference = 2 × π × 3
- Circumference ≈ 2 × 3.1416 × 3
- Circumference ≈ 18.85 units
Angles in a Triangle

All angles in a triangle sum to 180 degrees. Here's how to solve for missing angles:
| Known Angles | Missing Angle | Calculation |
|---|---|---|
| 45°, 90° | x | 180° - (45° + 90°) = 45° |
| 75°, 30° | x | 180° - (75° + 30°) = 75° |
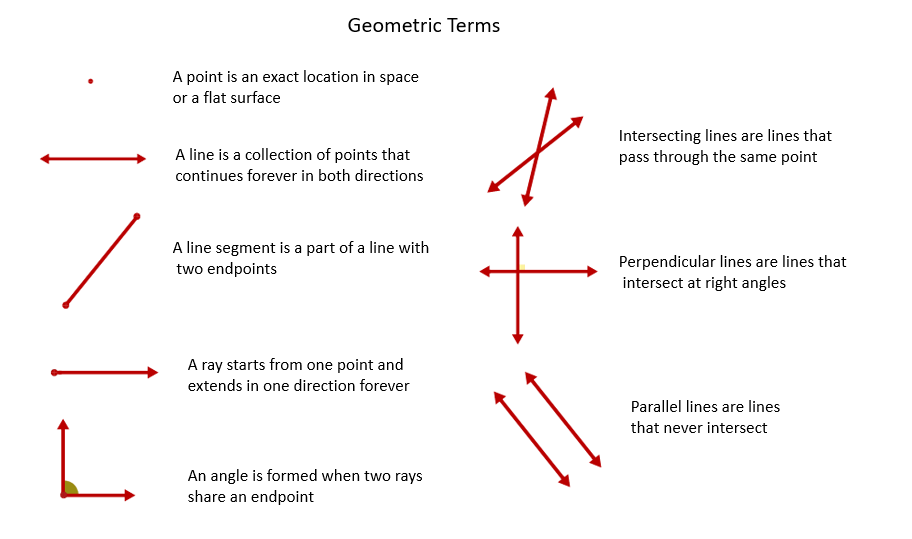
⚠️ Note: While these methods are fundamental, always double-check your work for accuracy in real-world scenarios.
In summary, understanding the basics of geometry through these simple worksheet solutions can provide you with a solid foundation. From calculating areas to understanding angles, these principles are not just for academic exercises but are crucial in numerous practical applications. Whether you're working on DIY projects or just want to sharpen your math skills, these solutions offer a clear path to better grasp geometry.
Why is it important to understand the basics of geometry?
+
Geometry is crucial for practical applications in design, architecture, engineering, and many other fields where spatial understanding is essential.
Can you apply geometry principles outside of mathematics?

+
Absolutely. Geometry helps in creating visual art, planning layouts, understanding geographic landscapes, and even in everyday tasks like tiling or painting walls.
What if I forget these formulas?

+
With practice, these formulas become second nature. However, keeping a reference sheet handy or using online tools can serve as useful reminders.



