Geometry Basics Worksheet: Master Fundamentals Easily

Introduction to Geometry Basics

Geometry, the mathematical study of shapes and their properties, has been a fundamental part of education for centuries. In this geometry basics worksheet, we aim to guide you through understanding and mastering the essentials of this discipline in a fun, engaging, and comprehensive way.

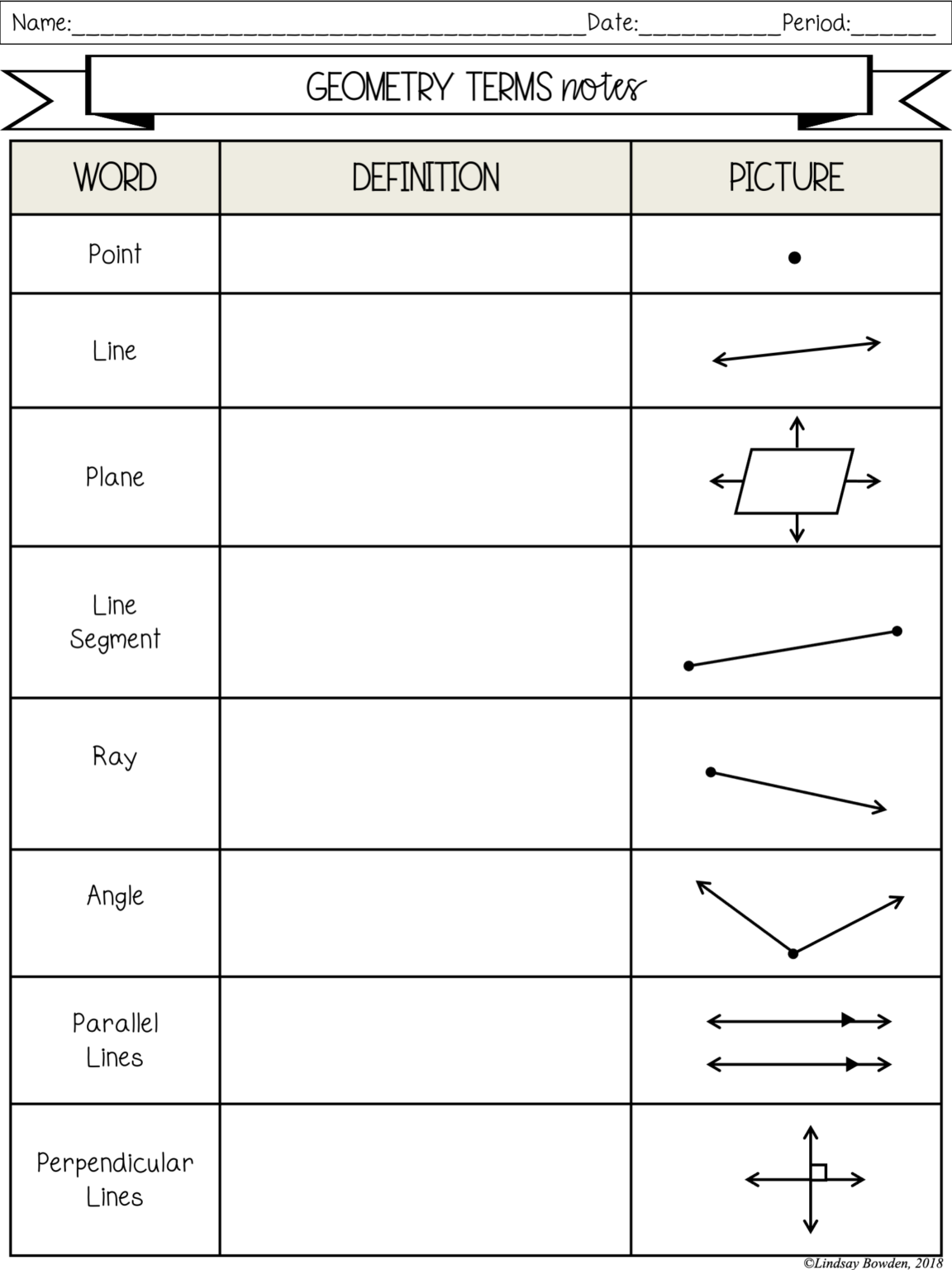
1. Key Points and Lines

Geometry starts with understanding the basic elements of any shape:
- Points: These are zero-dimensional entities, indicating a location in space.
- Lines: They are one-dimensional figures extending infinitely in two directions. Lines can be described as straight or curved, but for our purposes, we’ll focus on straight lines.

2. Angles: The Basics

Angles are formed when two lines intersect at a point:
- Acute Angle: Less than 90 degrees.
- Right Angle: Exactly 90 degrees, typically denoted by a small square at the vertex.
- Obtuse Angle: Between 90 and 180 degrees.
- Straight Angle: Exactly 180 degrees, forming a straight line.

3. Triangles and Their Properties

Triangles are fundamental shapes in geometry:
- Types: Equilateral, isosceles, and scalene, each defined by the lengths of their sides.
- Angle Sum Property: The sum of the interior angles in a triangle is always 180 degrees.
- Pythagorean Theorem: For right-angled triangles, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

4. Quadrilaterals

A quadrilateral is a four-sided polygon. Here are some common types:
- Square: All sides equal, all angles 90 degrees.
- Rectangle: Opposite sides equal, all angles 90 degrees.
- Parallelogram: Opposite sides parallel and equal in length.
- Trapezoid: Exactly one pair of parallel sides.
- Rhombus: All sides equal, opposite angles equal.

5. Perimeter and Area
Understanding how to calculate the perimeter and area is crucial:
- Perimeter: The total length of all the sides of a polygon.
- Area: The space enclosed by the polygon, measured in square units.
| Shape | Perimeter Formula | Area Formula |
|---|---|---|
| Triangle | a + b + c | (1⁄2) * base * height |
| Square | 4 * side | side2 |
| Rectangle | 2 * (length + width) | length * width |

✍️ Note: Remember, these formulas are just the basics; many shapes require more complex calculations for their area.
6. Circles and Pi

Circles are defined by their radius or diameter:
- Circumference: 2 * π * radius or π * diameter
- Area: π * radius2

7. Coordinate Geometry
Coordinate geometry involves plotting points on a coordinate plane:
- Distance Formula: d = √((x2 - x1)2 + (y2 - y1)2)
- Slope: (y2 - y1) / (x2 - x1)
⚠️ Note: Remember to check the order of subtraction when calculating slopes to get the correct sign.
To wrap up our exploration of geometry basics, we've covered a wide array of topics from points and lines to coordinate geometry. This foundational knowledge not only equips you to solve geometric problems but also prepares you for more complex geometry in your educational journey. Geometry is not just about numbers and shapes; it's about understanding the world around us through a mathematical lens, enhancing our spatial reasoning, and deepening our appreciation for patterns and symmetry. Keep practicing with geometric exercises, and remember, every shape has a story, every angle a narrative, and every coordinate a purpose in the grand design of mathematics.
What’s the difference between a polygon and a polyhedron?

+
A polygon is a flat, two-dimensional shape with straight sides, like a triangle or square. A polyhedron, however, is a three-dimensional shape with flat polygonal surfaces, edges, and vertices, like a cube or pyramid.
How do I calculate the area of a complex shape?

+
For complex shapes, you can break them down into simpler geometric figures whose areas you know how to calculate. Add these areas together to get the total area. For shapes that don’t divide neatly, consider using calculus or numerical methods for a more accurate area estimation.
Can geometry be applied to real-world problems?

+
Absolutely! Geometry is used in fields like architecture, engineering, computer graphics, and even in everyday tasks like mapping or design. It helps in understanding structures, optimizing space, calculating distances, and much more.



