Geometry Basics: Segment Addition Postulate Worksheet Answers

Geometry is a fundamental branch of mathematics that explores shapes, sizes, and positions of figures. At its core, understanding how different parts of geometric figures interact with each other is essential, particularly when dealing with segments. The Segment Addition Postulate is one of the key concepts students learn, which helps in understanding how to find the length of segments that share a common endpoint. Here, we delve deep into this postulate, provide comprehensive answers to common worksheet problems, and explore its applications.
Understanding the Segment Addition Postulate

The Segment Addition Postulate essentially states that if three points, A, B, and C, are collinear such that point B lies between A and C, then the distance from A to B plus the distance from B to C equals the distance from A to C. Mathematically, this is expressed as:
- AB + BC = AC
Applications of the Segment Addition Postulate

This postulate is not just an abstract concept; it has practical applications in:
- Designing road layouts: Engineers use it to segment the construction of highways or city streets.
- Surveying and Mapping: Surveyors use segment addition to plot land boundaries or determine distances between points.
- Computer Graphics: Artists and programmers use segment addition to create accurate animations and renderings.
Key Principles

- Linearity: Points must be collinear for the postulate to apply.
- Additivity: The distances can be added only when segments are adjacent.
- Precision: All measurements must be accurate to ensure correct calculations.
Worksheet Answers: A Practical Guide

Here we will address some typical problems from segment addition postulate worksheets:
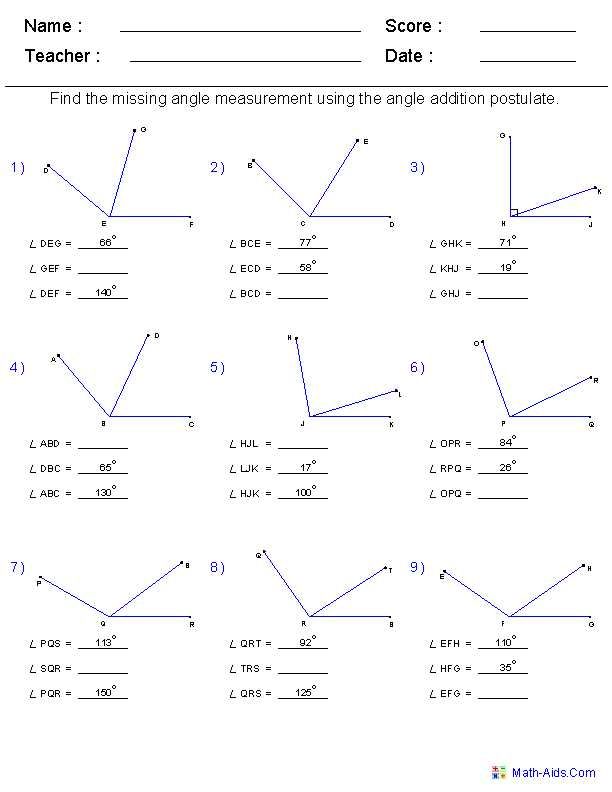
Problem 1: Basic Segment Addition

If point B is between points A and C with AB = 5 units and AC = 12 units, what is the length of segment BC?
📝 Note: Ensure all measurements are precise, and verify that B is indeed between A and C.
Solution:
- AB + BC = AC
- 5 + BC = 12
- BC = 12 - 5
- BC = 7 units
Problem 2: Finding Unknown Segments
If AB = 8 units, BC = x units, and AC = 15 units, find the value of x.
Solution:
- AB + BC = AC
- 8 + x = 15
- x = 15 - 8
- x = 7 units
Problem 3: Extended Segment Addition

If segments AB, BC, and CD are collinear, and you know AB = 3 units, BC = 4 units, CD = 2 units, what is the length of AD?
Solution:
- AB + BC + CD = AD
- 3 + 4 + 2 = 9 units
💡 Note: Be careful with segments that are not immediately adjacent but are still collinear.
Notes on Solving Segment Addition Problems

- Ensure you understand the collinearity of points.
- Always confirm the intermediate points are between the outer points.
- Check your arithmetic twice for accuracy.
In summary, mastering the Segment Addition Postulate provides a foundational understanding that aids in higher-level geometric concepts, practical applications in engineering and design, and even in everyday tasks requiring measurements. The ability to add segments accurately is not just about solving textbook problems; it’s about cultivating an intuitive sense of space and dimension, which is invaluable in numerous fields.
What is the Segment Addition Postulate?
+
The Segment Addition Postulate states that if B is between A and C on a straight line, then AB + BC = AC.
Can the Segment Addition Postulate be applied if points are not collinear?

+
No, the postulate applies only when points are on the same straight line. If points are not collinear, the distances cannot be directly added.
How can I ensure I’m applying the postulate correctly?

+
Check that the point you’re adding is indeed between the other two, ensure collinearity, and confirm all measurements are accurate.
Is there a visual method to understand segment addition?

+
Yes, use a ruler or a straightedge to draw a line segment and physically mark the points. Measure the segments to visually confirm the addition.
What are some common mistakes in segment addition?

+
Common mistakes include: adding non-adjacent segments, assuming collinearity when points are not in a straight line, and arithmetic errors in the addition.